Đề bài
Cho một tam giác vuông. Biết tỷ số hai cạnh góc vuông là \(3 : 4\) và cạnh huyền là \(125cm\). Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\).
Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\)
+) \(A{C^2} = CH.BC\)
+) \(AB^2+AC^2=BC^2\) (định lý Pytago).
Lời giải chi tiết
Giả sử \(\Delta ABC\) vuông tại \(A\) chiều cao \(AH, BC=125cm\) và \(\dfrac{{AB}}{{AC}} = \dfrac{3}{4}\)
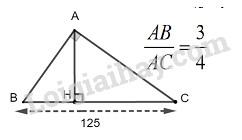
Từ \(\dfrac{{AB}}{{AC}} = \dfrac{3 }{4}\) suy ra: \(\dfrac{{AB}}{{3}} = \dfrac{{AC}}{4} \Rightarrow \dfrac{{A{B^2}}}{{ 9}} = \dfrac{{A{C^2}}}{{16}}\)
Theo tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{{A{B^2}}}{9} = \dfrac{{A{C^2}}}{{16}}\)\( = \dfrac{{A{B^2} + A{C^2}}}{{9 + 16}} = \dfrac{{A{B^2} + A{C^2}}}{{25}}\, (1)\)
Theo định lí Pytago, ta có:
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& \Rightarrow A{B^2} + A{C^2} = {125^2} = 15625\,(2) \cr} \)
Từ (1) và (2) suy ra: \(\dfrac{{A{B^2}}}{9} = \dfrac{{A{C^2}}}{{16}}\)\( = \dfrac{{A{B^2} + A{C^2}}}{{25}} = \dfrac{{15625}}{{25}} = 625\)
Suy ra :
\(A{B^2} = 9.625 = 5625\)\( \Rightarrow AB = \sqrt {5625} = 75(cm)\)
\(A{C^2} = 16.625 = 10000\)\( \Rightarrow AC = \sqrt {10000} = 100(cm)\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(A{B^2} = BH.BC\)\( \Rightarrow BH = \dfrac{{A{B^2}}}{{BC}} \)\(= \dfrac{{{{75}^2}}}{{125}} = 45(cm)\)
\(CH = BC - BH\)\( = 125 - 45 = 80(cm).\)
soanvan.me
