Đề bài
Biểu thức tổng quát của hàm số có đồ thị như hình \(1.6\) là:
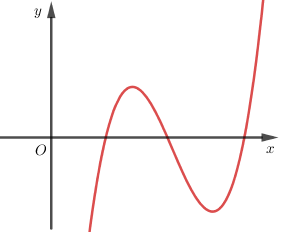
A. \(y = a{x^2} + bx + c\) với \(a \ne 0\).
B. \(y = a{x^3} + cx + d\) với \(a < 0\).
C. \(y = a{x^3} + b{x^2} + cx + d\) với \(a > 0\) và \({b^2} - 3ac > 0\).
D. \(y = {x^3}\).
Phương pháp giải - Xem chi tiết
- Nhận xét dáng đồ thị, số điểm cực trị và loại đáp án.
Lời giải chi tiết
Quan sát dáng đồ thị ta thấy:
+ Đây là đồ thị hàm đa thức bậc ba. Loại A.
+ Có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \) nên hệ số \(a > 0\). Loại B.
+ Đáp án D có \(y' = 3{x^2} \ge 0,\forall x\) nên hàm số đồng biến trên \(\mathbb{R}\) và không có cực trị nên loại D.
Chọn C.
Chú ý:
Đáp án C có \(y' = 3a{x^2} + 2bx + c\) và \(\Delta ' = {b^2} - 3ac > 0\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt hay đồ thị hàm số có hai điểm cực trị.
soanvan.me
