Đề bài
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:
y = 0,5x + 2 (1)
y = 5 – 2x (2)
b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tìm tọa độ của các điểm A, B, C
c) Tính độ dài các đoạn AB, AC và BC (đơn vị đi trên các trục tọa độ là xentimet) (làm tròn đến chữ số thấp phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).
Phương pháp giải - Xem chi tiết
a) Cách vẽ đường thẳng y = ax + b (trường hợp \(a \ne 0\) và \(b \ne 0\))
- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.
- Cho y = 0 thì \(x = - \dfrac{b}{a}\), được điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P và Q.
b) Tìm hoành độ giao điểm rồi thay vào một trong hai hàm số để tìm giá trị của tung độ giao điểm.
Lời giải chi tiết
a) Vẽ đồ thị hàm số \(y = 0,5x + 2\) :
Cho \(x = 0\) thì \(y=2\), được điểm \(D\left( {0;2} \right)\)
Cho \(y = 0\) thì \(x = - 4\), được điểm \(A\left( { - 4;0} \right)\)
Vẽ đường thẳng đi qua hai điểm A, D được đồ thị hàm số \(y = 0,5x + 2\).
- Vẽ đồ thị hàm số \(y = 5 - 2x\) :
Cho \(x = 0\) thì \(y = 5\), được điểm \(E\left( {0;5} \right)\)
Cho \(y = 0\) thì \(x = \dfrac{5}{2}\), được điểm \(B\left( {\dfrac{5}{2};0} \right)\)
Vẽ đường thẳng đi qua hai điểm B, E, được đồ thị hàm số \(y = 5 - 2x\).
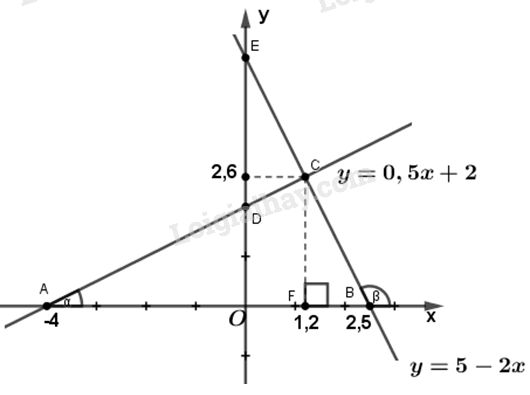
b) Ở câu a) đã tính được tọa độ của hai điểm A và B là \(A\left( { - 4;0} \right)\) và \(B\left( {\dfrac{5}{2};0} \right)\).
Ta tìm tọa độ của điểm C :
- Tìm hoành độ của điểm C:
\(0,5x + 2 = 5 - 2x \Leftrightarrow x = \dfrac{6}{5}\)
- Tìm tung độ của điểm C (thay \(x = \dfrac{6}{5}\) vào một trong hai hàm số), ta có :
\(y = 0,5 \cdot \dfrac{6}{5} + 2 = \dfrac{{13}}{5}\)
Vậy ta có : \(C\left( {\dfrac{6}{5};\dfrac{{13}}{5}} \right)\)
c) \(AB = AO + OB \)\(= \left| { - 4} \right| + \left| {2,5} \right| = 6,5\)
Gọi F là hình chiếu của C trên Ox, ta có \({\rm{OF}} = 1,2\left( {cm} \right)\), \({\rm{AF}} = 5,2\left( {cm} \right)\), \(BF = 1,3\left( {cm} \right)\).
Áp dụng định lí Py-ta-go vào các tam giác vuông ACF và BCF, ta có :
\(AC = \sqrt {A{F^2} + C{F^2}} = \sqrt {5,{2^2} + 2,{6^2}} \) \( \approx 5,8\left( {cm} \right)\)
\(BC = \sqrt {B{F^2} + C{F^2}} = \sqrt {1,{3^2} + 2,{6^2}} \)\( \approx 2,9\left( {cm} \right)\)
d) Gọi \(\alpha \) là góc tạo bởi đường thẳng \(y = 0,5x + 2\) và trục Ox, ta có :
\(\tan \alpha = 0,5 \Rightarrow \alpha \approx {26^o}33'\)
Gọi \(\beta \) là góc tạo bởi đường thẳng \(y = 5 - 2x\) với trục \({\rm{Ox}}\), ta có :
\(\tan \left( {{{180}^o} - \beta } \right) = \left| { - 2} \right| \)\(\Rightarrow {180^o} - \beta \approx {63^o}26'\) \( \Rightarrow \beta \approx {180^o} - {63^o}26' \approx {116^o}34'\).
soanvan.me
