Đề bài
Cho tam giác Abc cân tại A có góc A nhọn và H là trực tâm. Cho biết \(\widehat {BHC} = {150^o}\). Tính các góc của tam giác ABC.
Phương pháp giải - Xem chi tiết
- Áp dụng: tổng ba góc trong một tam giác bằng \({180^o}\) và đường cao trong tam giác để tính các số đo góc.
Lời giải chi tiết
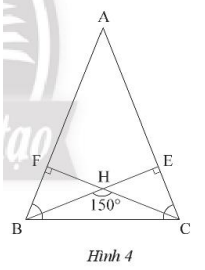
Vẽ hai đường cao BE và CF của tam giác ABC.
Xét tam giác BHC ta có:
\(\widehat {HBC} + \widehat {HCB} = {180^o} - {150^o} = {30^o}\)
Xét hai tam giác vuông BCF và CBE ta có:
\(\widehat B + \widehat C = {180^o} - \left( {\widehat {HBC} + \widehat {HCB}} \right) = {180^o} - {30^o} = {150^o}\)
Do tam giác ABC cân tại A nên ta có:
\(\widehat B = \widehat C = \frac{{{{150}^o}}}{2} = {75^o}\)
\(\widehat {{A^{}}} = {180^o} - {150^o} = {30^o}\)
