Đề bài
Tính diện tích hình thang cân, biết hai cạnh đáy là \(12\,cm\) và \(18\,cm,\) góc ở đáy bằng \(75\)\(^\circ \)
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích hình thang: \(S=\dfrac{a+b}{2}.h\)
Áp dụng các hệ thức về cạnh và góc trong tam giác vuông, tam giác \(ABC\) vuông tại \(A\) có \(AB=c,\,AC=b,\, BC=a\) thì:
\(b=a.sin\,B=a.cos\,C\)
\(b=c.tan\,B=c.cot\,C\)
\(c=a.sin\,C=a.cos\,B\)
\(c=b.tan\,C=b.cot\,B\)
Lời giải chi tiết
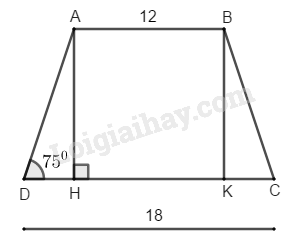
Giả sử hình thang cân \(ABCD\) có \(AB = 12\,cm,\, CD = 18\,cm,\) \(\widehat D = 75^\circ \)
Kẻ \(AH \bot CD,BK \bot CD\) suy ra \(AH//BK\)
Lại có \(AB//HK\) nên ABKH là hình bình hành.
Suy ra: \(AB = HK = 12\, (cm)\)
Vì \(ABCD\) là hình thang cân nên \(\widehat D = \widehat C,AD=BC\)
Nên \(\Delta ADH = \Delta BCK\) (cạnh huyền, góc nhọn)
Suy ra: \(DH = CK\) (2 cạnh tương ứng)
Suy ra:
\(CK=DH = \dfrac{CD - HK} {2} = \dfrac{18 - 12}{2} \) \(= 3\,(cm)\)
Trong tam giác vuông \(ADH,\) ta có:
\(AH = DH.tgD = 3.tg75^\circ \) \(\approx 11,196\,(cm)\)
Vậy:
\(\eqalign{
& {S_{ABCD}} = {{AB + CD} \over 2}.AH \cr
& \approx {{12 + 18} \over 2}.11,196 = 167,94 cm^2.\cr} \)
