Đề bài
Cho tam giác ABC có ba góc nhọn, các đường cao BH, CK. Gọi D, E lần lượt là hình chiếu của B và C lên đường thẳng HK. Gọi M là trung điểm của BC.
a) Chứng minh \(\Delta MKH\) cân.
b) Chứng minh DK = HE.
Phương pháp giải - Xem chi tiết
- Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
- Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
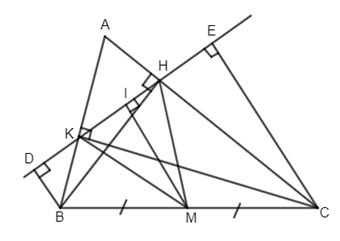
a) Ta có MH, MK là các trung tuyến của các tam giác vuông BHC và BKC có chung cạnh huyền BC nên \(MH = MK\) \((=\dfrac{BC}2)\)
Vậy \(\Delta MKH\) cân.
b) Kẻ \(MI \bot DE\)
Ta có: \(BD//MI//CE\) (cùng vuông góc với DE)
Suy ra BDEC là hình thang có \(BD//MI//CE\) và M là trung điểm BC
\( \Rightarrow I\) là trung điểm của DE hay \(ID = IE\;\;(1)\)
Mặt khác \(\Delta MKH\) cân có đường cao MI đồng thời là trung tuyến nên IK = IH (2)
Từ (1) và (2) \( \Rightarrow ID - IK = IE - IH\) hay \(DK = HE.\)
soanvan.me
