Đề bài
Dựng hình thang ABCD \(\left( {AB//CD} \right)\) biết: AB = 1,5cm; CD = 3,5cm; \(\widehat C = {45^ \circ };\widehat D = {60^ \circ }\)
Phương pháp giải - Xem chi tiết
+) Cách dựng: Nêu thứ tự từng bước dựng hình, đồng thời thể hiện các nét dựng trên hình vẽ.
+) Chứng minh: Bằng lập luận để chứng tỏ rằng với cách dựng trên, hình đã dựng thỏa mãn các điều kiện của đề bài nêu ra.
+) Biện luận: Xem xét khi nào bài toán dựng được và dựng được bao nhiêu hình thỏa mãn đề bài
Lời giải chi tiết
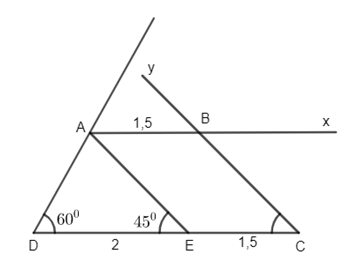
Phân tích: Giả sử đã dựng được hình thang ABCD thỏa mãn. Kẻ \(AE//BC \Rightarrow \widehat {AED} = {45^ \circ }\) và \(DE = DC - EC = DC - AB\)\(\; = 3,5 - 1,5 = 2cm\) nên \(\Delta ADE\) dựng được.
Cách dựng:
-Dựng \(\Delta ADE\) biết \(DE = 2cm;\widehat D = {60^ \circ },\widehat E = {45^ \circ }.\)
-Trên tia DE lấy C sao cho DC = 3,5 cm. Cần xác định đỉnh B.
-B thuộc tia \({\rm{Ax}}//CD.\)
-B thuộc tia Cy mà \(\widehat {DCy} = {45^ \circ }.\)
Lấy điểm B là giao điểm của tia Ax và Cy ta được hình thang ABCD cần dựng.
Chứng minh:
Theo cách dựng ta có AB//DC nên ABCD là hình thang
Và AB =EC= 1,5cm; CD = 3,5cm; \(\widehat C = {45^ \circ };\widehat D = {60^ \circ }\) nên hình thang ABCD thỏa mãn đề bài.
Biện luận: Luôn vẽ được một hình thang thỏa mãn đề bài.
soanvan.me
