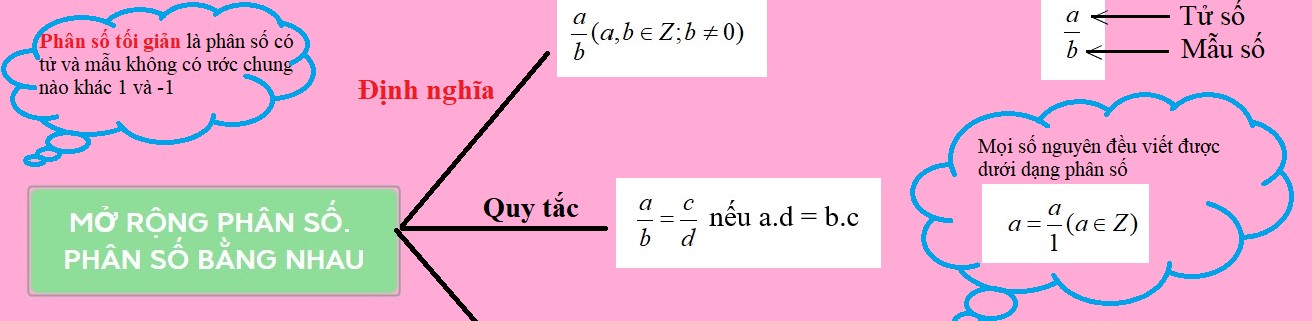Lý thuyết Phân số với tử số và mẫu số là nguyên

I. Mở rộng khái niệm phân số

Ví dụ 1:

\(\dfrac{2}{5};\,\dfrac{{ - 3}}{4};\dfrac{{ - 1}}{{ - 7}};...\) là những phân số

Ví dụ 2:

Phân số \(\dfrac{{ - 4}}{7}\) đọc là: Âm bốn phần bảy, có tử số là \( - 4\) và mẫu số là \(7\).

Chú ý:

+ Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu.

+ Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.

II. Phân số bằng nhau

a) Khái niệm hai phân số bằng nhau

Hai phân số bằng nhau nếu chúng cùng biểu diễn một giá trị.

b) Quy tắc bằng nhau của hai phân số

Xét hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\)

Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\). Ngược lại, nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\)

Ví dụ:

Do \(3.5 = ( - 5).( - 3)\) nên \(\dfrac{3}{{ - 5}} = \dfrac{{ - 3}}{5}\)

Do \(2.\left( { - 3} \right) \ne 5.7\) nên \(\dfrac{2}{5} \ne \dfrac{7}{{ - 3}}\)

Chú ý:

Với \(a,b\) là hai số nguyên và \(b \ne 0\), ta luôn có: \(\dfrac{a}{{ - b}} = \dfrac{{ - a}}{b}\) và \(\dfrac{{ - a}}{{ - b}} = \dfrac{a}{b}\).

III. Biểu diễn số nguyên ở dạng phân số

Mỗi số nguyên \(n\) có thể coi là phân số \(\dfrac{n}{1}\) (Viết \(\dfrac{n}{1} = n\)). Khi đó số nguyên \(n\) được biểu diễn diễn ở dạng phân số \(\dfrac{n}{1}\).

Ví dụ:

\(\dfrac{{ - 14}}{1} = - 14;\,\,\,\,\,52 = \dfrac{{52}}{1}\).

CÁC DẠNG TOÁN VỀ PHÂN SỐ VỚI TỬ SỐ VÀ MẪU SỐ NGUYÊN 

I. Nhận biết phân số, đọc các phân số, mô tả các bài toán thực tiễn qua phân số

- Sử dụng định nghĩa phân số:

Người ta gọi \(\dfrac{a}{b}\) với \(a,b \in Z;b \ne 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.

- Quan sát hình vẽ hoặc dựa vào các dự kiện đề bài ra để mô tả các bài toán thực tiễn qua phân số. Ý nghĩa tử số và mẫu số của phân số:
+) Mẫu số cho biết đơn vị được chia ra làm mấy phần bằng nhau 
+) Tử số cho biết số phần bằng nhau đã lấy.

Chú ý: Mẫu của phân số phải khác 0.

II. Nhận biết các cặp phân số bằng nhau, không bằng nhau

- Nếu \(a.d = b.c\) thì \(\dfrac{a}{b} = \dfrac{c}{d}\);

- Nếu \(a.d \ne b.c\) thì \(\dfrac{a}{b} \ne \)\(\dfrac{c}{d}\);

III. Tìm số chưa biết trong đẳng thức của hai phân số

\(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) nên \(a.d = b.c\) (định nghĩa hai phân số bằng nhau)

Suy ra \(a = \dfrac{{b.c}}{d}\) , \(d = \dfrac{{b.c}}{a}\) , \(b = \dfrac{{a.d}}{c}\) , \(c = \dfrac{{a.d}}{b}.\)

IV. Lập các cặp phân số bằng nhau từ một đẳng thức cho trước

Từ định nghĩa phân số bằng nhau ta có:

\(a.d = b.c\) \( \Rightarrow \) \(\dfrac{a}{b}\) = \(\dfrac{c}{d}\) ;

\(a.d = c.b\) \( \Rightarrow \) \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\) ;

\(d.a = b.c\) \( \Rightarrow \) \(\dfrac{d}{b}\) = \(\dfrac{c}{a}\) ;

\(d.a = c.b\) \( \Rightarrow \) \(\dfrac{d}{c}\) = \(\dfrac{b}{a}\) ;