Mục 1 trang 125 SGK Vật lí 9

a.

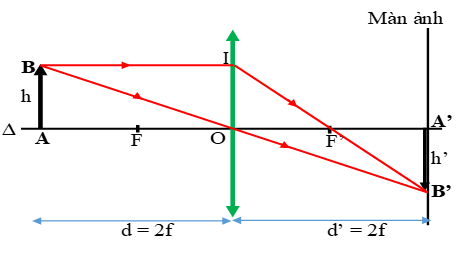
Dựng ảnh của một vật AB có độ cao là h và vuông góc với trục chính của TKHT và cách thấu kính một khoảng d = 2f.

Lời giải chi tiết:

b.

Dựa vào hình vẽ để chứng minh rằng trong trường hợp này thì ta thu được ảnh ngược chiều cao bằng vật và khoảng cách từ vật và từ ảnh đến thấu kính là bằng nhau (d’ = 2f).

Lời giải chi tiết:

Ta có \(BI = AO = 2f = 2OF'\) , nên \(OF'\)  là đường trung bình của \(\Delta B'BI\).

Từ đó suy ra \(OB = OB'\).

Lại có \(\widehat {BOA} = \widehat {B'OA'}\) (góc đối đỉnh);  \(AB \bot AO\) và \(A'B' \bot OA'\)

Vậy \(\Delta ABO = \Delta A'B'O\) (theo trường hợp cạnh huyền và một góc nhọn bằng nhau)

Kết quả, ta có \(A'B' = h' = h = AB\) và \(OA'{\rm{ }} = {\rm{ }}OA{\rm{ }} = {\rm{ }}2f\). (đpcm)

c.

Ảnh này có kích thước như thế nào so với vật?

Lời giải chi tiết:

Ảnh thật A’B’ có kích thước bằng vật: AB = A'B' hay h = h'.

d.

Công thức tính tiêu cự thấu kính trong trường hợp này?

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}OA' = OA = 2f\\ \Rightarrow d' = d = 2f\\ \Rightarrow f = \dfrac{{d + d'}}{4}\end{array}\)

e.

Tóm tắt các bước tiến hành đo tiêu cự thấu kính hội tụ theo phương pháp này.

Lời giải chi tiết:

+ Đo chiều cao của vật, đánh dấu chiều cao này trên màn ảnh.

+ Dịch chuyển vật và màn ảnh ra xa thấu kính những khoảng bằng nhau cho đến khi thu được ảnh rõ nét

+ Kiểm tra lại xem các điều kiện d = d’ và h = h’ có thỏa mãn hay không.

+ Tính tiêu cự của thấu kính theo công thức: \(f = \dfrac{{d + d'}}{4}\)

soanvan.me