Dòng điện xoay chiều qua một đoạn mạch có tần số dao động là $f$. Mỗi giây dòng điện đổi chiều bao nhiêu lần?
-
A
$0,5f$
-
B
$f$
-
C
$2f$
-
D
$4f$
Đáp án của giáo viên lời giải hay : C
Trong mỗi giây: Dòng điện đổi chiều $2f$ lần
Từ thông qua khung dây có biểu thức: \(\Phi = {\Phi _0}\cos 40\pi t\). Trong $1s$ dòng điện trong khung dây đổi chiều:
-
A
$20$ lần
-
B
$40$ lần
-
C
$60$ lần
-
D
$80$ lần
Đáp án của giáo viên lời giải hay : B
Ta có, trong mỗi giây dòng điện đổi chiều $2f$ lần
Từ biểu thức:
\(\Phi = {\Phi _0}\cos 40\pi t\),
ta có
$\omega = 40\pi \to f = \dfrac{\omega }{{2\pi }} = \dfrac{{40\pi }}{{2\pi }} = 20(H{\text{z}})$
=> Trong $1s$ dòng điện đổi chiều $2f = 2.20 = 40$ lần
Dòng điện xoay chiều qua một đoạn mạch có biểu thức $i = {I_0}{\text{cos}}\left( {120\pi t - \dfrac{\pi }{2}} \right)A$. Trong $2,5s$ dòng điện đổi chiều bao nhiêu lần?
-
A
$149$
-
B
$150$
-
C
$299$
-
D
$300$
Đáp án của giáo viên lời giải hay : C
Từ biểu thức cường độ dòng điện:
$i = {I_0}{\text{cos}}\left( {120\pi t - \dfrac{\pi }{2}} \right)A$
Ta có: tần số
$f = \dfrac{\omega }{{2\pi }} = \dfrac{{120\pi }}{{2\pi }} = 60(H{\text{z}})$
Ta có: Nếu pha ban đầu ${\varphi _i} = \dfrac{\pi }{2}$ hoặc ${\varphi _i} = - \dfrac{\pi }{2}$
thì chỉ giây đầu tiên đổi chiều 2f-1 lần
=> Trong 2,5s , dòng điện đổi chiều:
$2,5(2f) - 1 = 2,5.(2.60) - 1 = 299$ lần
Tại thời điểm t, điện áp $u = 200\sqrt 2 {\text{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)$ (trong đó u tính bằng V, t tính bằng s) có giá trị $100\sqrt 2 $ và đang giảm. Sau thời điểm đó $\dfrac{1}{{300}}s$, điện áp này có giá trị là:
-
A
\(-100V\)
-
B
$100\sqrt 3 V$
-
C
$ - 100\sqrt 2 V$
-
D
\(200V\)
Đáp án của giáo viên lời giải hay : C
Sử dụng vòng tròn lượng giác
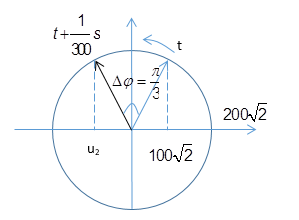
Xác định các điểm trên vòng tròn lượng giác, ta được:
Góc quay từ t đến $\dfrac{1}{{300}}s$ :
$\Delta \varphi = \omega \Delta t = 100\pi \dfrac{1}{{300}} = \dfrac{\pi }{3}(ra{\text{d}})$
Từ vòng tròn ta có:
Tại thời điểm $t + \dfrac{1}{{300}}s$ điện áp có giá trị: ${u_2} = - 100\sqrt 2 (V)$
Vào cùng một thời điểm nào đó, hai dòng điện xoay chiều \({i_1} = {I_0}cos(\omega t + {\varphi _1})\) và \({i_2} = {I_0}cos(\omega t + {\varphi _2})\) đều có cùng giá trị tức thời là 0,5I0 nhưng một dòng điện đang giảm, còn một dòng điện đang tăng. Hai dòng điện này lệch pha nhau một góc bằng:
-
A
$\dfrac{{5\pi }}{6}$
-
B
$\dfrac{{2\pi }}{3}$
-
C
$\dfrac{\pi }{6}$
-
D
$\dfrac{{4\pi }}{3}$
Đáp án của giáo viên lời giải hay : B
Sử dụng vòng tròn lượng giác
Vẽ vòng tròn lượng giác, ta được:
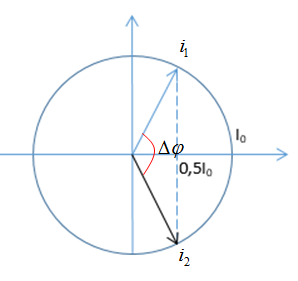
Từ vòng tròn lượng giác ta có, độ lệch pha giữa hai dòng điện này là:
$\Delta \varphi = \dfrac{{2\pi }}{3}$
Dòng điện xoay chiều qua một đoạn mạch có biểu thức $i = {I_0}{\text{cos}}\left( {120\pi t - \dfrac{\pi }{3}} \right)A$ thời điểm thứ 2009 cường độ dồng điện tức thời có độ lớn bằng cường độ hiệu dụng là:
-
A
$\dfrac{{12049}}{{1440}}s$
-
B
$\dfrac{{24097}}{{1440}}s$
-
C
$\dfrac{{24113}}{{1440}}s$
-
D
Đáp án khác
Đáp án của giáo viên lời giải hay : A
+ Sử dụng công thức tính chu kì dao động: $T = \dfrac{{2\pi }}{\omega }$
+ Sử dụng vòng tròn lượng giác
+ \({t_{2009}} = {\text{ }}{t_{2008}} + {\text{ }}{t_1}\)

Ta có:
+ Chu kì dao động :
$T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{120\pi }} = \dfrac{1}{{60}}s$
+ t2009 = t2008 + t1
Trong 1 chu kì, cường độ dòng điện có độ lớn bằng cường độ hiệu dụng 4 lần
\( \to {t_{2008}} = \dfrac{{2008}}{4}T = 502T\)
Tại t = 0:
$i = {I_0}{\text{cos}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{{{I_0}}}{2}$
\({t_1} = \dfrac{T}{8} - \dfrac{T}{{12}} = \dfrac{T}{{24}}\)
\( \to {t_{2009}} = {t_{2008}} + {t_1} = 502T + \dfrac{T}{{24}} = \dfrac{{12049}}{{24}}T = \dfrac{{12049}}{{1440}}(s)\)
Điện áp tức thời giữa hai đầu đoạn mạch có biểu thức: $u = 240\sin \left( {100\pi t} \right)V$. Thời điểm gần nhất sau đó để điện áp tức thời đạt giá trị \(120V\) kể từ thời điểm ban đầu là:
-
A
$\dfrac{1}{{600}}s$
-
B
$\dfrac{1}{{100}}s$
-
C
$\dfrac{1}{{50}}s$
-
D
$\dfrac{1}{{300}}s$
Đáp án của giáo viên lời giải hay : A
+ Sử dụng công thức tính chu kì dao động: $T = \dfrac{{2\pi }}{\omega }$
+ Sử dụng vòng tròn lượng giác

Biểu thức điện áp hai đầu đoạn mạch:
\(u = 240\sin 100\pi t\left( V \right)= 240\cos \left( {100\pi t - \frac{\pi }{2}}\right)\left( V \right)\)
Chu kì dao động :
$T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{100\pi }} = 0,02s$
Tại $t = 0$:
$u = 0(V)$
Thời điểm gần nhất sau đó để điện áp tức thời đạt giá trị $120V$ kể từ thời điểm ban đầu là: $t = \dfrac{T}{{12}} = \dfrac{{0,02}}{{12}} = \dfrac{1}{{600}}s$
Dòng điện chạy qua một đoạn mạch có biểu thức $i = {I_0}{\text{cos}}\left( {100\pi t} \right)A$. Trong khoảng thời gian từ 0 đến 0,01s cường độ dòng điện tức thời trong có độ lớn bằng 0,5I0 vào những thời điểm:
-
A
$\dfrac{1}{{400}}s$ và $\dfrac{2}{{400}}s$
-
B
$\dfrac{1}{{500}}s$ và $\dfrac{3}{{500}}s$
-
C
$\dfrac{1}{{300}}s$ và $\dfrac{2}{{300}}s$
-
D
$\dfrac{1}{{600}}s$ và $\dfrac{5}{{600}}s$
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức: $\Delta \varphi = \omega \Delta t$
+ Sử dụng vòng tròn lượng giác
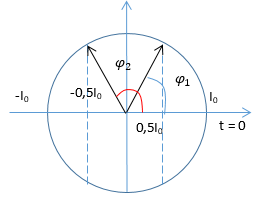
Ta có, từ thời điểm 0 - 0,01s thì góc quay được là:
$\Delta \varphi = \omega \Delta t = 100\pi .0,01 = \pi (ra{\text{d}})$
Tại t = 0:
$i = {I_0}{\text{cos0 = }}{I_0}(A)$
Từ vòng tròn lượng giác ta có:
+ ${\varphi _1} = \omega {t_1} = \dfrac{\pi }{3} \to {t_1} = \dfrac{1}{{300}}s$
+ ${\varphi _2} = \omega {t_2} = \dfrac{{2\pi }}{3} \to {t_2} = \dfrac{2}{{300}}s$
Dòng điện xoay chiều \(i = 2sin100\pi t{\text{ }}A\) qua một dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là:
-
A
0
-
B
$\dfrac{4}{{100\pi }}C$
-
C
$\dfrac{3}{{100\pi }}C$
-
D
$\dfrac{6}{{100\pi }}C$
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức tính điện lượng :
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\text{d}}t} \)
+ Cách 1: (Phương pháp đại số)
Ta có, điện lượng chạy qua tiết diện dây:
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\text{d}}t} = \int\limits_0^{0,15} {2sin(100\pi t){\text{d}}t} \\= \dfrac{{ - 2}}{{100\pi }}{\text{cos(100}}\pi {\text{t)}}\left| {_0^{0,15}} \right. \\= \dfrac{{ - 2}}{{100\pi }}( - 1 - 1) = \dfrac{4}{{100\pi }} = \dfrac{1}{{25\pi }}\)
+ Cách 2: Sử dụng máy tính Casio fx-570 ES Plus
Bấm ghi vào màn hình \(\int\limits_0^{0,15} {2\sin \left( {100\pi x} \right)} dx\) ấn \( = \)
Ta thu được kết quả: \(0,0127323\) trên màn hình
Với cách này chú ý giữa chế độ D (Độ) và R (Rad) trên máy tính để bấm máy phù hợp với chế độ đang cài đặt của máy.
Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức cường độ là
$i = {I_0}{\text{cos}}\left( {\omega t - \dfrac{\pi }{2}} \right)A$ , I0>0. Tính từ lúc t=0(s), điện lượng chuyển qua tiết diện phẳng của dây dẫn của đoạn mạch đó trong thời gian bằng nửa chu kì của dòng điện là:
-
A
0
-
B
$\dfrac{{2{I_0}}}{\omega }$
-
C
$\dfrac{{\pi \sqrt 2 {I_0}}}{\omega }$
-
D
$\dfrac{{\pi {I_0}}}{{\omega \sqrt 2 }}$
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức tính điện lượng :
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\text{d}}t} \)
Ta có, điện lượng chạy qua tiết diện dây:
\(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\text{d}}t} = \int\limits_0^{\frac{T}{2}} {{I_0}{\text{cos}}\left( {\omega t - \dfrac{\pi }{2}} \right){\text{d}}t} = \dfrac{{{I_0}}}{\omega }{\text{sin}}\left( {\omega t - \dfrac{\pi }{2}} \right)\left| {_0^{\dfrac{T}{2}}} \right. = \dfrac{{{I_0}}}{\omega }(1 - ( - 1)) = \dfrac{{2{I_0}}}{\omega }\)
Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức cường độ là $i = {I_0}{\text{cos}}\left( {\omega t + \varphi } \right)A$, I0>0. Điện lượng chuyển qua tiết diện thẳng của dây dẫn đoạn mạch đó trong thời gian bằng chu kì của dòng điện là:
-
A
$0$
-
B
$\dfrac{{2{I_0}}}{\omega }$
-
C
$\dfrac{{\pi \sqrt 2 {I_0}}}{\omega }$
-
D
$\dfrac{{\pi {I_0}}}{{\omega \sqrt 2 }}$
Đáp án của giáo viên lời giải hay : A
Ta có: Điện lượng qua tiết diện S trong 1 chu kì bằng 0
Một chiếc đèn neon đặt dưới một điện áp xoay chiều $119V-50Hz$. Nó chỉ sáng lên khi điện áp tức thời giữa hai đầu bóng đèn có trị tuyệt đối lớn hơn $84V$. Thời gian bóng đèn sáng trong một chu kì là bao nhiêu?
-
A
\(\Delta t = 0,0100s\)
-
B
\(\Delta t = 0,0133s\)
-
C
\(\Delta t = 0,0200s\)
-
D
\(\Delta t = 0,0233s\)
Đáp án của giáo viên lời giải hay : B
+ Nhận biết cách ghi các thông số trên đèn
+ Sử dụng vòng tròn lượng giác
+ Vận dụng biểu thức tính tần số góc:
$\omega = 2\pi f$
+ Vận dụng biểu thức:
\(\Delta \varphi = \omega \Delta t\)
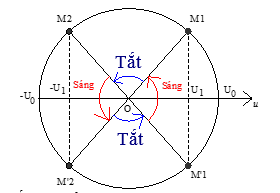
Ta có:
+ Hiệu điện thế cực đại:
${U_0} = 119\sqrt 2 (V)$
+ Tần số góc:
$\omega = 2\pi f = 2\pi .50 = 100\pi (ra{\text{d}}/s)$
+ Vẽ trên vòng tròn lượng giác, ta được:
Biết đèn chỉ sáng lên khi u ≥ U1
Ta có:
+ $c{\text{os}}\Delta \varphi = \frac{{{U_1}}}{{{U_0}}} = \frac{{84}}{{119\sqrt 2 }} \approx 0,5 \to \Delta \varphi = \frac{\pi }{3}$
Thời gian đèn sáng trong 1 chu kì:
$\Delta t = \frac{{4\Delta \varphi }}{\omega } = \frac{{4\frac{\pi }{3}}}{{100\pi }} = \frac{1}{{75}}s \approx 0,01333(s)$
Đặt điện áp xoay chiều có giá trị hiệu dụng $U=120V$, tần số $f=60Hz$ vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn $60\sqrt 2 V$. Thời gian đèn sáng trong mỗi giây là:
-
A
$\dfrac{1}{2}s$
-
B
$\dfrac{1}{3}s$
-
C
$\dfrac{2}{3}s$
-
D
$\dfrac{1}{4}s$
Đáp án của giáo viên lời giải hay : C
+ Sử dụng vòng tròn lượng giác
+ Vận dụng biểu thức tính tần số góc: $\omega = 2\pi f$
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
Ta có:
+ Hiệu điện thế cực đại:
${U_0} = 120\sqrt 2 (V)$
+ Tần số góc:
$\omega = 2\pi f = 2\pi .60 = 120\pi (ra{\text{d}}/s)$
+ Vẽ trên vòng tròn lượng giác, ta được:
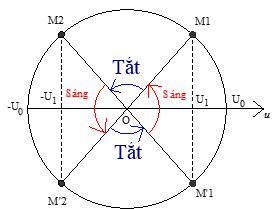
Biết đèn chỉ sáng lên khi u ≥ U1
Ta có:
+ $c{\text{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{60\sqrt 2 }}{{120\sqrt 2 }} = 0,5 \to \Delta \varphi = \dfrac{\pi }{3}$
Thời gian đèn sáng trong 1 chu kì:
$\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{3}}}{{120\pi }} = \dfrac{1}{{90}}s$
Ta có:
+ Chu kì: $T = \dfrac{1}{f} = \dfrac{1}{{60}}s$
+ $1{\text{s}} = 60T$
=> Thời gian đèn sáng trong 1s là:
$t = \Delta t.60 = 60.\dfrac{1}{{90}} = \dfrac{2}{3}s$
Đặt điện áp xoay chiều có giá trị hiệu dụng \(U=120V\), tần số \(f = 60Hz\) vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn $60\sqrt 2 V$. Tỉ số thời gian đèn sáng và đèn tắt trong \(30\) phút là:
-
A
2
-
B
0,5
-
C
3
-
D
1/3
Đáp án của giáo viên lời giải hay : A
+ Sử dụng vòng tròn lượng giác
+ Vận dụng biểu thức tính tần số góc: $\omega = 2\pi f$
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
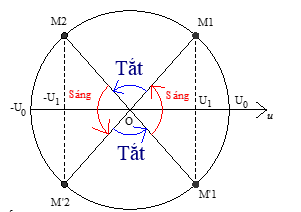
Ta có:
+ Hiệu điện thế cực đại: ${U_0} = 120\sqrt 2 (V)$
+ Tần số góc: $\omega = 2\pi f = 2\pi .60 = 120\pi (ra{\text{d}}/s)$
+ Vẽ trên vòng tròn lượng giác, ta được:
Biết đèn chỉ sáng lên khi u ≥ U1
Ta có:
+ $c{\text{os}}\Delta \varphi = \dfrac{{{U_1}}}{{{U_0}}} = \dfrac{{60\sqrt 2 }}{{120\sqrt 2 }} = 0,5 \to \Delta \varphi = \frac{\pi }{3}$
Thời gian đèn sáng trong 1 chu kì:
$\Delta t = \dfrac{{4\Delta \varphi }}{\omega } = \dfrac{{4\dfrac{\pi }{3}}}{{120\pi }} = \dfrac{1}{{90}}s$
Thời gian đèn tắt trong 1 chu kì:
\(\Delta t' = T - \Delta t = \dfrac{1}{{60}} - \dfrac{1}{{90}} = \dfrac{1}{{180}}s\)
Ta có:
+ Chu kì
$T = \dfrac{1}{f} = \dfrac{1}{{60}}s$
+ $t = 30' = 30.60s = 108000T$
=> Thời gian đèn sáng trong 30’ là: ${t_1} = t.\Delta t$
Thời gian đèn tắt trong 30’ là: ${t_2} = t.\Delta t'$
Tỉ số thời gian đèn sáng và đèn tắt trong 30 phút là:
$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{\dfrac{1}{{90}}}}{{\dfrac{1}{{180}}}} = 2$
Một khung dây quay đều trong từ trường đều quanh một trục vuông góc với đường cảm ứng từ. Suất điện động hiệu dụng trong khung là 60V. Nếu giảm tốc độ quay của khung đi 2 lần nhưng tăng cảm ứng từ lên 3 lần thì suất điện động hiệu dụng trong khung có giá trị là:
-
A
150V
-
B
120V
-
C
60V
-
D
90V
Đáp án của giáo viên lời giải hay : D
Suất điện động hiệu dụng trong khung: \(E = \dfrac{{\omega {\Phi _0}}}{{\sqrt 2 }} = \dfrac{{\omega .B.S.cos\alpha }}{{\sqrt 2 }}\)
Theo bài ra ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}E = \dfrac{{\omega .B.S.cos\alpha }}{{\sqrt 2 }} = 60V\\E = \dfrac{{\omega '.B'.S.cos\alpha }}{{\sqrt 2 }} = \dfrac{{\dfrac{\omega }{2}.3B.S\cos \alpha }}{{\sqrt 2 }} = 1,5E\end{array} \right.\\ \Rightarrow E = 1,5.60 = 90V\end{array}\)
Một đèn nêon mắc với mạch điện xoay chiều có điện áp hiệu dụng \(220V\) và tần số \(50Hz\). Biết đèn sáng khi điện áp giữa hai cực không nhỏ hơn \(155V\). Trong một giây, bao nhiêu lần đèn chớp sáng, đèn chớp tắt?
-
A
50 lần chớp sáng, 100 lần chớp tắt
-
B
100 lần chớp sáng, 50 lần chớp tắt.
-
C
100 lần chớp sáng, 100 lần chớp tắt.
-
D
50 lần chớp sáng, 50 lần chớp tắt.
Đáp án của giáo viên lời giải hay : C
Sử dụng lí thuyết về dao động của con lắc lò xo
Trong 1 chu kì đèn chớp sáng 2 lần và chớp tắt 2 lần
\(T = \dfrac{1}{f} = \dfrac{1}{{50}} = 0,02s\)
\(1s = 50T\)
\( \Rightarrow \) Trong 1 giây đèn chớp sáng 100 lần và chớp tắt 100 lần.
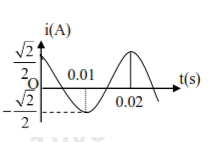
Đồ thị hình bên mô tả sự biến thiên của cường độ dòng điện xoay chiều theo thời gian. Biểu thức của cường độ dòng điện tức thời có biểu thức
-
A
\(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A.\)
-
B
\(i = 2cos\left( {100\pi t} \right)A.\)
-
C
\(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A.\)
-
D
\(i = 1cos\left( {100\pi t} \right)A.\)
Đáp án của giáo viên lời giải hay : C
+ Đọc đồ thị i-t
+ Sử dụng biểu thức \(\omega = \dfrac{{2\pi }}{T}\)
+ Viết phương trình cường độ dòng điện
Từ đồ thị ta có:
+ Cường độ dòng điện cực đại: \({I_0} = \dfrac{{\sqrt 2 }}{2}A\)
+ Chu kì dao động: \(T = 0,02s\)
\( \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,02}} = 100\pi \)
+ Tại thời điểm ban đầu, dòng điện có giá trị cực đại: \( \Rightarrow {i_0} = {I_0}cos\varphi = {I_0} \Rightarrow cos\varphi = 1 \Rightarrow \varphi = 0\)
\( \Rightarrow \) Phương trình cường độ dòng điện: \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A\)
Tại thời điểm t, điện áp \(u=200\sqrt{2}\text{cos(100}\pi \text{t-}\frac{\pi }{2})\) (trong đó u tính bằng V, t tính bằng s) có giá trị bằng \(100\sqrt{2}V\) và đang giảm. Sau thời điểm đó 1/300 (s) điện áp này có giá trị
-
A
-100V
-
B
200V
-
C
\(-100\sqrt{2}V\)
-
D
\(100\sqrt{3}V\)
Đáp án của giáo viên lời giải hay : C
Chu kỳ dao động: \(T=\frac{2\pi }{\omega }\)
Điện áp có U0 = \(200\sqrt{2}V\) và pha ban đầu – π/2
Thời điểm có u = \(100\sqrt{2}V\) và đang giảm ứng với vị trí góc π/3
Chu kỳ \(T=\frac{2\pi }{\omega }=0,02s\)
Sau đó 1/300s = T/6 ứng với vị trí góc 2π/3 nên điện áp có giá trị - \(100\sqrt{2}V\)
