Đặt điện áp \(u = 180\sqrt 2 {\rm{cos}}\omega {\rm{t (V)}}\) (với \(\omega \) không đổi) vào hai đầu đoạn mạch AB gồm đoạn mạch AM nối tiếp đoạn mạch MB. Đoạn mạch AM có điện trở thuần R, đoạn mạch MB có cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C mắc nối tiếp. Điện áp hiệu dụng ở hai đầu đoạn mạch AM và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi \(L = {L_1}\) là \(U\) và \({\varphi _1}\), còn khi \(L = {L_2}\) thì tương ứng là \(\sqrt 8 U\) và \({\varphi _2}\) . Biết \({\varphi _1} + {\varphi _2} = {90^0}\). Hệ số công suất của mạch khi \(L = {L_1}\) là:
-
A
\(0,33\)
-
B
\(0,86\)
-
C
\(0,5\)
-
D
\(0,71\)
Đáp án của giáo viên lời giải hay : A
+ Vận dụng công thức lượng giác: ${\varphi _1} + {\varphi _2} = \dfrac{\pi }{2} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = {\rm{}}1$
+ Vận dụng công thức: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
+ Vận dụng biểu thức: \(U = {\rm{IZ}}\)
+ Sử dụng biểu thức tính hệ số công suất: \({\rm{cos}}\varphi = \dfrac{R}{Z}\)
Ta có:
+ Khi $L = {L_1}$ thì ${U_{A{M_1}}} = {U_{{R_1}}} = U$
+ Khi $L = {L_2}$ thì ${U_{AM2}} = \;{U_{R2}} = \sqrt 8 U$
${\varphi _1} + {\varphi _2} = \dfrac{\pi }{2} \to \tan {\varphi _1}\tan {\varphi _2} = {\text{}} - 1 \to \dfrac{{{Z_{L1}} - {Z_{C1}}}}{R}.\dfrac{{{Z_{L2}} - {Z_{C2}}}}{R} = {\text{}} - 1{\text{ }}(1)$
Mặt khác, ta có:
$\begin{array}{l}\dfrac{{{U_{R1}}}}{{{U_{R2}}}} = \dfrac{1}{{\sqrt 8 }} \to {I_2} = \sqrt 8 {I_1} \to {Z_1} = \sqrt 8 {Z_2}\\ \leftrightarrow \sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} = \sqrt 8 \sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_C}} \right)}^2}} \\ \leftrightarrow {\left( {{Z_{L1}} - {Z_C}} \right)^2} - 7{R^2} - 8{\left( {{Z_{L2}} - {Z_C}} \right)^2} = 0({\rm{2}})\end{array}$
Chia cả hai vế của (2) cho kết hợp với (1), ta được:
$\dfrac{{{{\left( {{Z_{L1}} - {Z_C}} \right)}^2}}}{{{{\left( {{Z_{L2}} - {Z_C}} \right)}^2}}} - 7\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} - 8 = 0 \to \left[ \begin{array}{l}\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = 1(Loai)\\\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = - 8\end{array} \right.$
Với $\dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{{\left( {{Z_{L2}} - {Z_C}} \right)}} = {\text{}} - 8 \to {\text{}} - \dfrac{{\left( {{Z_{L1}} - {Z_C}} \right)}}{8} = \left( {{Z_{L2}} - {Z_C}} \right)$
Thay vào (1) => ${\left( {{Z_{L1}} - {Z_C}} \right)^2} = 8{R^2}$
Hệ số công suất của mạch khi $L = {L_1}$ : ${\rm{cos}}{\varphi _1} = \dfrac{R}{{{Z_1}}} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_C}} \right)}^2}} }} = \dfrac{R}{{3R}} = \dfrac{1}{3}$
Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là \(75\% \). Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá \(40\% \). Nếu công suất sử dụng điện của khu dân cư này tăng \(25\% \) và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây đó là:
-
A
\(65,8\% \)
-
B
\(79,2\% \)
-
C
\(62,5\% \)
-
D
\(87,7\% \)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính công suất hao phí trên đường dây: \(\Delta P = \dfrac{{{P^2}R}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\)
\(\Delta P = \dfrac{{{P^2}R}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }} = {P^2}x\) ( \(x = \dfrac{R}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\)không đổi)
Ban đầu: \(\dfrac{{\Delta P}}{P} = P{\rm{x}} = 1 - H = 1 - 0,75 = 0,25\)
Sau khi công suất sử dụng tăng lên $25\% $:
$\begin{array}{l}P' - \Delta P' = 1,25(P - \Delta P) = 0,9375P\\ \to P' - {P^2}x = 0,937P\\ \to \dfrac{{P'}}{P} - {P^2}.P\dfrac{{0,25}}{P} = 0,9375\end{array}$
Đặt $\dfrac{{P'}}{P} = k$ , ta có: $k - 0,25{k^2} = 0,9375 \to \left[ \begin{array}{l}k = 2,5\\k = 1,5\end{array} \right.$
Với $k = 2,5$, ta suy ra:
\(H = 1 - \dfrac{{\Delta P'}}{{P'}} = 1 - P'x = 1 - 2,5P{\rm{x}} = 0,375 = 37,5\% \) (loại vì hao phí không quá 40%)
Với $k{\rm{ }} = {\rm{ }}1,5$, ta suy ra:
\(H = 1 - \dfrac{{\Delta P'}}{{P'}} = 1 - P'x = 1 - 1,5P{\rm{x}} = 0,625 = 62,5\% \)
Cho dòng điện xoay chiều chạy qua đoạn mạch AB có sơ đồ như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức lần lượt \({u_{AN}} = 30\sqrt 2 cos\omega t(V);{u_{MB}} = 40\sqrt 2 cos\left( {\omega t - \frac{{\pi {\rm{}}}}{2}} \right)(V)\)
Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là:
![]()
-
A
\(16{\rm{ }}V\)
-
B
\(50V\)
-
C
\(32V\)
-
D
\(24V\)
Đáp án của giáo viên lời giải hay : D
Sử dụng giản đồ vecto và hệ thức lượng trong tam giác vuông
\({u_{AN}} = {u_L} + {u_X}\)
\({u_{MB}} = {u_C} + {u_X}\)
\({u_{AB}} = {u_{AN}} + {u_C}\)
\({U_{AB}} \ge OH \to \left( {{U_{AB}}} \right)min = OH\)
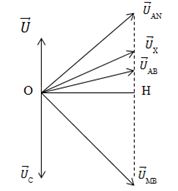
Áp dụng hệ thức lượng trong tam giác vuông ta có : \(\frac{1}{{U_{AB}^2}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}} \Rightarrow {U_{AB}} = 24V\)
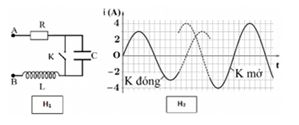
Đặt điện áp xoay chiều \(u = {U_0}cos\left( {\omega t + \varphi } \right)\) vào hai đầu đoạn mạch AB gồm điện trở , tụ điện và cuộn cảm thuần mắc nối tiếp (hình \({H_1}\) ). Ban đầu khóa K đóng, sau đó khóa K mở. Hình \({H_2}\) là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch vào thời gian t. Giá trị của \({U_0}\) gần nhất với giá trị nào sau đây?
-
A
\(170{\rm{ }}V\)
-
B
\(212{\rm{ }}V\)
-
C
\(127{\rm{ }}V\)
-
D
\(255{\rm{ }}V\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng công thức
\({I_0} = \dfrac{{{U_0}}}{Z}\)
+ Sử dụng công thức tính độ lệch pha
\(tan\varphi = \dfrac{{\left( {{Z_L}-{\rm{ }}{Z_C}} \right)}}{R}\)
+ Kĩ năng đọc đồ thị
\(\begin{array}{l}\dfrac{{U_0^2}}{{{3^2}}} = R_0^2 + Z_L^2 \Rightarrow Z_L^2 = \dfrac{{U_0^2}}{{{3^2}}} - 5,76\\\dfrac{{U_0^2}}{{{4^2}}} = R_0^2 + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = \dfrac{{U_0^2}}{{{4^2}}} - 5,76{R^2} = {Z_L}\left( {{Z_L} - {Z_C}} \right)\\ \Rightarrow \dfrac{{{R^2}}}{{Z_L^2}} = \dfrac{{{Z_L} - {Z_C}}}{{{Z_L}}} \Rightarrow \dfrac{{\dfrac{{U_0^2}}{{{4^2}}} - 5,76}}{{\dfrac{{U_0^2}}{{{3^2}}} - 5,76}} = {\left( {\dfrac{{{R^2}}}{{Z_L^2}}} \right)^2}\end{array}\)
\(\begin{array}{l} \Rightarrow \left( {\dfrac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4}\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right)\\ \Rightarrow \left( {\dfrac{{U_0^2}}{{{4^2}}} - 5,76} \right)\left( {\dfrac{{U_0^2}}{{{3^2}}} - 5,76} \right) = {R^4} \Rightarrow \dfrac{{U_0^4}}{{{3^2}{{.4}^2}}} - 5,76\left( {\dfrac{{U_0^2}}{{{3^2}}} + \dfrac{{U_0^2}}{{{4^2}}}} \right) = 0\\ \Rightarrow {U_0} = R\sqrt {{3^2} + {4^2}} = 120V\end{array}\)
Đặt điện áp \(u = {U_0}{\rm{cos100}}\pi {\rm{t}}\left( V \right)\) (t tính bằng s) vào đoạn mạch gồm cuộn dây và tụ điện mắc nối tiếp. Cuộn dây có độ tự cảm \(L = \frac{{1,5}}{\pi }H\), điện trở \(r = 50\sqrt 3 \Omega \), tụ điện có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }F\) . Tại thời điểm \({t_1}\), điện áp tức thời giữa hai đầu cuộn dây có giá trị \(150V\), đến thời điểm \({t_1} + \frac{1}{{75}}s\) thì điện áp giữa hai đầu tụ điện cũng bằng \(150V\). Giá trị của \({U_0}\) bằng:
-
A
\(150\sqrt 3 V\)
-
B
\(100\sqrt 3 V\)
-
C
\(300{\rm{ }}V\)
-
D
\(150V\)
Đáp án của giáo viên lời giải hay : B
+ Viết phương trình u, i
+ Vận dụng công thức lượng giác
Ta có:
\(\begin{array}{l}{Z_L} = \omega L = 150\Omega ;{Z_C} = \dfrac{1}{{\omega C}} = 100\Omega ;r = 50\sqrt 3 \Omega \\Z = 100\Omega ;{Z_d} = \sqrt {{r^2} + {Z_L}^2} = 100\sqrt 3 \end{array}\)
\(\begin{array}{l}i = \dfrac{{{U_0}}}{Z}{\rm{cos}}\left( {\omega t - \dfrac{\pi }{6}} \right) = 0,01{U_0}{\rm{cos}}\left( {\omega t - \dfrac{\pi }{6}} \right)\\{u_d} = {I_0}{{\rm{Z}}_d}{\rm{cos}}\left( {\omega t + \dfrac{\pi }{6}} \right) = {U_0}\sqrt 3 {\rm{cos}}\left( {\omega t + \dfrac{\pi }{6}} \right)\\{u_C} = {I_0}{Z_C}{\rm{cos}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right) = {U_0}{\rm{cos}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right)\end{array}\)
${u_d} = {U_0}\sqrt 3 {\text{cos}}\left( {\omega {t_1} + \dfrac{{\pi {\text{}}}}{6}} \right) = 150V{\text{ }}({\text{1}})$
Tại thời điểm \({t_2} = {t_1} + \dfrac{1}{{75}}s\), ta có: ${u_C} = {U_0}{\text{cos}}\left( {\omega \left( {{t_1} + \dfrac{1}{{75}}} \right) - \dfrac{{2\pi }}{3}} \right) = {U_0}{\text{cos}}\left( {\omega {t_1} + \dfrac{{2\pi }}{3}} \right) = {U_0}\sin \left( {\omega {t_1} + \dfrac{{\pi {\text{}}}}{6}} \right) = 150V{\text{ }}({\text{2}})$
Từ (1) và (2), ta có: ${\left( {\dfrac{{{u_d}}}{{\sqrt 3 }}} \right)^2} + {\left( {{u_C}} \right)^2} = U_0^2 \leftrightarrow \dfrac{{{{150}^2}}}{3} + {150^2} = U_0^2{\rm{ }} \to {U_0} = 100\sqrt 3 {\rm{ }}$
Cho mạch điện xoay chiều gồm điện trở thuần R, tụ điện có điện dung C và cuộn dây có độ tự cảm L mắc nối tiếp theo thứ tự đó. Biết tụ điện có điện dung C có thể thay đổi được, khi \(C = {C_1} = \dfrac{{62,5}}{\pi }\mu F\) điện áp hai đầu mạch \(U = 150V\) thì mạch tiêu thụ công suất cực đại \({P_{max}} = 93,75{\rm{ }}W\). Khi \(C = {C_1} = \dfrac{1}{{9\pi }}\mu F\) thì điện áp hiệu dụng trên hai đầu đoạn mạch chứa điện trở thuần và tụ điện \(\left( {{u_{RC}}} \right)\) và cuộn dây \(\left( {{u_d}} \right)\) vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó là:
-
A
\(75V\)
-
B
\(120V\)
-
C
\(90V\)
-
D
\(75\sqrt 2 V\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng công thức tính công suất: \(P = UI\cos \varphi \)
+ C biến thiên để \({P_{{\rm{max}}}}\) hay \({I_{{\rm{max}}}}\) khi \({Z_L} = {Z_C}\)
+ Sử dụng biểu thức định luật ôm: \(I = \dfrac{U}{Z}\)
+ Bài toán \({U_{RL}} \bot {U_{RC}}\)
Ta có \(u = 150\sqrt 2 .\cos (100\pi t)V \to \omega = 100\pi \)
Khi \(C = {C_1} = \dfrac{{62,5}}{\pi }\mu F\) thì , \({Z_{{C_1}}} = \dfrac{1}{{\omega {C_1}}} = 160\Omega \)
\({P_{max}}\) khi \({I_{max}}\) có xảy ra cộng hưởng => \({Z_L} = {Z_C} = 160\Omega \)
\(P = {I^2}R = \dfrac{{{U^2}}}{{{Z^2}}}.R = \dfrac{{{U^2}.{R_m}}}{{{R_m}^2 + {{({Z_L} - {Z_C})}^2}}}\)
Thay số từ đề bài \(P = 93,75W;U = 150V\) ; ta tính được
\(C = {C_2} = \dfrac{1}{{9\pi }}\mu F = > {Z_{{C_2}}} = 90\Omega \) thì \({U_d}\) vuông pha với \({U_{RC}}\)
\({U_d}\) vuông pha với \({U_{RC}}\) cho ta biết cuộn dây có điện trở trong \(r\).
\(I = \dfrac{U}{Z} = \frac{U}{{\sqrt {{R^2} + ({Z_L} - {Z_{{C_2}}})} }} = \dfrac{{150}}{{\sqrt {{{240}^2} + {{(160 - 90)}^2}} }} = 0,6A\)
Vì \({U_{Lr}}\) vuông góc với \({U_{RC}}\) nên: \(U_{Lr}^2 + U_{RC}^2 = {150^2}U_L^2 + U_r^2 + U_R^2 + U_C^2 = {150^2}\)
Mặt khác theo định luật Ôm ta có:
\(\begin{array}{l}U_{Rr}^2 + {(U_L^{} - {U_C})^2} = {U^2} = {150^2}{({U_R} + {U_r})^2} + {({U_L} - {U_C})^2}\\ = {150^2}U_R^2 + 2{U_R}{U_r} + U_r^2 + U_L^2 + U_L^2 - 2.{U_L}.{U_C} = {150^2}{U_R}.{U_r} - {U_L}{U_C} = 0\\ = > r.R - {Z_L}.{Z_C} = 0 = > r.R = {Z_L}.{Z_C} = 160.90\end{array}\)
\(\left\{ {\begin{array}{*{20}{l}}
{r.R = 160.90} \\
{r + R = 240}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{r = 120\Omega } \\
{R = 120\Omega {\text{}}}
\end{array}} \right.\)
\({U_d} = I.\sqrt {{r^2} + Z_L^2} = 0,6.\sqrt {{{120}^2} + {{160}^2}} = 120V\)
Điện năng được truyền từ nơi phát đến một xưởng sản xuất bằng đường dây một pha với hiệu suất truyền tải là \(90\% \). Ban đầu xưởng sản xuất này có \(90\) máy hoạt động, vì muốn mở rộng quy mô sản xuất nên xưởng đã nhập thêm về một số máy. Hiệu suất truyền tải lúc sau (khi có thêm các máy mới cùng hoạt động) đã giảm đi \(10\% \) so với ban đầu. Coi hao phí điện năng chỉ do toả nhiệt trên đường dây, công suất tiêu thụ điện của các máy hoạt động (kể cả các máy mới nhập về) đều như nhau và hệ số công suất trong các trường hợp đều bằng \(1\). Nếu giữ nguyên điện áp nơi phát thì số máy hoạt động đã được nhập về thêm là:
-
A
100
-
B
70
-
C
50
-
D
160
Đáp án của giáo viên lời giải hay : B
Sử dụng các công thức trong truyền tải điện năng :
+ Biểu thức tính điện năng hao phí: \(\Delta P = \frac{P}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}R\)
Do hiệu điện thế \(U\) không đổi nên: \(\frac{{\Delta {P_2}}}{{\Delta {P_1}}} = {(\frac{{{P_2}}}{{{P_1}}})^2} \to \frac{{{P_2}}}{{{P_1}}} = 2\)
\({H_1} = 90\% \)
\( \to {P_n} = 0,9{P_1} \to {P_0} = \frac{{{P_n}}}{{90}} = 0,01{P_1}\) (1)
Gọi \(x\) là số máy nhập thêm => công suất khi nhập mới:
\((90 + x).0,01{P_1} = 0,8{P_2} \to {P_2} = \frac{{(90 + x).0,01{P_1}}}{{0,8}}\) (2)
mà \({P_2} = 2{P_1}\) ,
\({\rm{}} \to \frac{{(90 + x).0,01{P_1}}}{{0,8}} = 2{P_1} \to (90 + x) = 160 \to x = 70\)
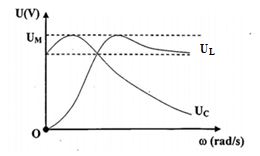
Đặt điện áp \(u = 200cos\omega t\left( V \right)\) (\(\omega \) thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm $L$, điện trở $R$ và tụ điện có điện dung $C$, với \(C{R^2} < 2L\). Điện áp hiệu dụng giữa hai bản tụ điện và điện áp hiệu dụng hai đầu cuộn cảm lần lượt là \({U_C},{U_L}\) phụ thuộc vào \(\omega \), chúng được biểu diễn bằng các đồ thị như hình vẽ bên, tương ứng với các đường \({U_C},{U_L}\). Giá trị của \({U_M}\) trong đồ thị gần nhất với giá trị nào sau đây?
-
A
\(160{\rm{ }}V\)
-
B
\(170{\rm{ }}V\)
-
C
\(120{\rm{ }}V\)
-
D
\(230{\rm{ }}V\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức \(\omega \) biến thiên để \({U_{Cm{\rm{ax}}}}\), khi đó: \({\omega _C} = \sqrt {\dfrac{{2L - {R^2}C}}{{2{L^2}C}}} \)
+ \(\omega = \dfrac{1}{{\sqrt {LC} }}\) : mạch cộng hưởng \({U_{Rm{\rm{ax}}}}\)
+ \(\omega \) biến thiên để \({U_{L\max }}\), khi đó: \({\omega _L} = \sqrt {\dfrac{2}{{2LC - {R^2}C}}} \)
Khi \(\omega {\rm{ }} = {\rm{ }}0\) thì \({U_C} = U\)
Khi \(\omega {\rm{}} = {\omega _C} = \sqrt {\dfrac{{2L - {R^2}C}}{{2{L^2}C}}} \)
thì \({U_C}\) cực đại
Khi \(\omega {\rm{}} = {\omega _R} = \sqrt {\dfrac{1}{{LC}}} \)
thì \({U_R}\) đạt cực đại bằng \(U\)
Khi \(\omega = 0\) thì \({U_L} = 0\) khi \(\omega {\rm{}} = {\omega _L} = \sqrt {\dfrac{2}{{2LC - {R^2}C}}} \)
thì \({U_{{L_{max}}}} = {U_M}\)
Đặt \(n = \dfrac{{{\omega _L}}}{{{\omega _C}}} = \dfrac{{2L}}{{2L - {R^2}C}} = {\rm{}} > \dfrac{1}{n} = 1 - \dfrac{{{R^2}C}}{{2L}} = 1 - \dfrac{{{R^2}}}{{2{Z_L}{Z_C}}};{\left( {\dfrac{U}{{{U_{{L_{max}}}}}}} \right)^2} + {\left( {\dfrac{1}{n}} \right)^2} = {\left( {\dfrac{U}{{{U_{{C_{max}}}}}}} \right)^2} + {\left( {\dfrac{1}{n}} \right)^2} = 1\)
Tại giao điểm của hai đồ thị, ta có \({U_L} = {U_C} = U\) (cộng hưởng )
\(\begin{array}{*{20}{l}}
{ = {\text{}} > \dfrac{1}{n} = 1 - \dfrac{{{R^2}}}{{2{Z_L}{Z_C}}} = 1 - \dfrac{{U_R^2}}{{2{U_L}{U_C}}} = 1 - \dfrac{{{U^2}}}{{2.U.U}} = \dfrac{1}{2} = {\text{}} > n = 2} \\
{{U_M} = {U_{{C_{max}}}} = {U_{{L_{max}}}} = \dfrac{{nU}}{{\sqrt {{n^2} - 1} }} = \dfrac{{2.100\sqrt 2 }}{{\sqrt {{2^2} - 1} }} = 163,3(V)}
\end{array}\)
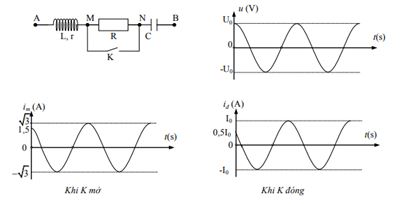
Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có đồ thị điện áp tức thời phụ thuộc vào thời gian như hình vẽ. Trong đó điện áp cực đại \({U_0}\) và chu kì dòng điện không thay đổi. Khi đóng và mở khóa K thì cường độ dòng điện tức thời trong mạch phụ thuộc vào thời gian như hình vẽ. Giá trị của \({I_0}\) là:
-
A
\(3\sqrt 3 A\)
-
B
\(3A\)
-
C
\(1,5\sqrt 3 A\)
-
D
\(2\sqrt 3 A\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng định luật Ôm
+ Sử dụng công thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
+ Khi khóa K mở, mạch gồm \(R,{\rm{ }}r,{\rm{ }}L,{\rm{ }}C\) nối tiếp
Từ đồ thị của điện áp, ta có: \(u = {U_0}.cos\omega t\)
Từ đồ thị cường độ dòng điện khi K mở ta có phương trình cường độ dòng điện là: \(i = {I_0}cos\left( {\omega t + {\varphi _i}_1} \right)\)
Khi \(t{\rm{ }} = {\rm{ }}0\):
\(\begin{array}{*{20}{l}}{i = 1,5 = \sqrt 3 .\cos {\varphi _{i1}} \Rightarrow {\varphi _{i1}} = \frac{\pi }{6} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{6}}\\{ \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{{R + r}} = \frac{{ - 1}}{{\sqrt 3 }} \Rightarrow {Z_L} - {Z_C} = \frac{{ - 1}}{{\sqrt 3 }}(R + r)}\end{array}\)
+ Khi K đóng, mạch có \(r,{\rm{ }}L,{\rm{ }}C\) nối tiếp
Ta có phương trình cường độ dòng điện là: \(i = {I_0}.cos\left( {\omega t + {\varphi _{i2}}} \right)\)
Khi \(t{\rm{ }} = {\rm{ }}0\):
\(\begin{array}{*{20}{l}}{i = 0,5{I_0} = {I_0}.\cos {\varphi _{i2}} \Rightarrow {\varphi _{i2}} = \frac{\pi }{3} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{3}}\\\begin{array}{l} \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{r} = - \sqrt 3 \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r\\ \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r = \frac{{ - 1}}{{\sqrt 3 }}(R + r) \Rightarrow R = 2r\end{array}\\{ \Rightarrow \left\{ \begin{array}{l}{Z_2} = \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} = 2r\\{Z_1} = \sqrt {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}} = 2\sqrt 3 r\end{array} \right.}\\{{I_{01}} = \frac{{{U_0}}}{{{Z_1}}};{I_{02}} = \frac{{{U_0}}}{{{Z_2}}} \Rightarrow \frac{{{I_{01}}}}{{{I_{02}}}} = \frac{{{Z_2}}}{{{Z_1}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {I_{02}} = {I_0} = 3A}\end{array}\)
Đặt một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu một đoạn mạch như hình vẽ. Khi K đóng, điều chỉnh giá trị biến trở đến giá trị \({R_1}\) hoặc \({R_2}\) thì công suất tỏa nhiệt trên mạch đều bằng \(P\). Độ lệch pha giữa điện áp tức thời hai đầu mạch và dòng điện trong mạch khi \(R = {R_1}\) là \({\varphi _1}\), khi \(R = {R_2}\) là \({\varphi _2}\) , trong đó \(\left| {{\varphi _1} - {\varphi _2}} \right| = \frac{\pi }{6}\) . Khi K mở, điều chỉnh giá trị \(R\) từ \(0\) đến rất lớn thì công suất tỏa nhiệt trên biến trở \(R\) cực đại bằng \(\frac{{2P}}{3}\), công suất trên cả mạch cực đại bằng \(\frac{{2P}}{{\sqrt 3 }}\). Hệ số công suất của cuộn dây là:
-
A
\(\frac{{\sqrt 3 }}{2}\)
-
B
\(\frac{1}{2}\)
-
C
\(\frac{{2\sqrt 3 }}{{\sqrt {13} }}\)
-
D
\(\frac{1}{{\sqrt {13} }}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng biến đổi toán học và các điều kiện P cực trị
+ Sử dụng biểu thức định luật ôm: \(I = \frac{U}{R}\)
+ Sử dụng công thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Khi K đóng, mạch chỉ có R, C mắc nối tiếp.
Khi \({R_1},{R_2}\) thì \({P_1} = {P_2}\) nên:
\(\begin{array}{*{20}{l}}{i = 0,5{I_0} = {I_0}.\cos {\varphi _{i2}} \Rightarrow {\varphi _{i2}} = \frac{\pi }{3} \Rightarrow \Delta {\varphi _m} = {\varphi _u} - {\varphi _{i1}} = \frac{{ - \pi }}{3}}\\\begin{array}{l} \Rightarrow \tan \Delta {\varphi _m} = \frac{{{Z_L} - {Z_C}}}{r} = - \sqrt 3 \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r\\ \Rightarrow {Z_L} - {Z_C} = - \sqrt 3 r = \frac{{ - 1}}{{\sqrt 3 }}(R + r) \Rightarrow R = 2r\end{array}\\{ \Rightarrow {Z_2} = \sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} = 2r;{Z_1} = \sqrt {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}} = 2\sqrt 3 r}\\{{I_{01}} = \frac{{{U_0}}}{{{Z_1}}};{I_{02}} = \frac{{{U_0}}}{{{Z_2}}} \Rightarrow \frac{{{I_{01}}}}{{{I_{02}}}} = \frac{{{Z_2}}}{{{Z_1}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {I_{02}} = {I_0} = 3A}\end{array}\)
Khi K mở thì mạch R, r, L, C nối tiếp Công suất mạch cực đại là:
\({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2({R_0} + r)}} = \frac{2}{{\sqrt 3 }}P \Rightarrow {Z_L} = 2{Z_C}\)
Công suất trên R cực đại: \({P_{R\max }} = \frac{{{U^2}}}{{2R}} = \frac{{2P}}{3} \Leftrightarrow {R^2} = {r^2} + {({Z_L} - {Z_C})^2} \Rightarrow r = \frac{{{Z_C}}}{{\sqrt 3 }}\)
Thay các giá trị tìm được vào tính hệ số công suất cuộn dây: \(\cos {\varphi _d} = \frac{r}{{\sqrt {{r^2} + {Z_L}^2} }} = \frac{1}{{\sqrt {13} }}\)
Lần lượt mắc một điện trở \(R\), một cuộn dây, một tụ điện \(C\) vào cùng một nguồn điện ổn định và đo cường đọ dòng điện qua chúng thì được các giá trị ( theo thứ tự ) là \(1A,{\rm{ }}1A\), và \(0A\); điện năng tiêu thụ trên \(R\) trong thời gian \(\Delta t\) khi đó là \(Q\). Sau đó mắc nối tiếp các linh kiện trên cùng với một ampe kế nhiệt lí tưởng vào một nguồn ổn định thứ hai thì số chỉ ampe kế là \(1A\). Biết nếu xét trong cùng thời gian \(\Delta t\) thì: điện năng tiêu thụ trên \(R\) khi chỉ mắc nó vào nguồn thứ hai là \(4Q\); còn khi mắc cuộn dây vào nguồn này thì điện năng tiêu thụ trong thời gian này cũng là \(Q\). Hỏi nếu mắc điện trở \(R\) nối tiếp với tụ và ampe kế nhiệt vào nguồn thứ hai thì ampe kế chỉ bao nhiêu?
-
A
\(1A\)
-
B
\(2A\)
-
C
\(\sqrt 2 A\)
-
D
\(0,5A\)
Đáp án của giáo viên lời giải hay : A
Sử dụng công thức tính điện năng tiêu thụ: \(Q = {I^2}Rt\)
+ Ban đầu cường độ dòng điện qua R. cuộn dây và C lần lượt là \(1A,1A,0A\), chứng tỏ dòng điện ban đầu là dòng điện không đổi, và cuộn dây có điện trở thuần bằng R sau đó dùng dòng điện xoay chiều.
Điện năng tiêu thụ ban đầu là : \(Q = \frac{{{U^2}}}{R}.\Delta t\)
Điện năng tiêu thụ khi đặt vào dòng điện lúc sau và chỉ có R là: \(Q' = \frac{{{U^2}}}{R}\Delta t = 4Q = 4.\frac{{{U^2}}}{R}{\rm{ }} = > U' = 2U{\rm{ }}\)
+ Khi cho dòng điện qua cuộn dây ta có:
\(\begin{array}{l}Q'' = \frac{{U{'^2}}}{{{{(R)}^2} + Z_L^2}}R.\Delta t = Q = \frac{{{U^2}}}{R}\Delta t\\ \leftrightarrow \frac{{4{U^2}}}{{{R^2} + Z_L^2}} = \frac{{{U^2}}}{R} \to {Z_L} = \sqrt 3 .R\end{array}\)
Khi mắc cả ba linh kiện vào dòng điện thừ 2 thì cường độ dòng điện là \(1A\).
Ta có: \(\frac{{U'}}{{\sqrt {{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{R}{\rm{ }} = > {Z_C} = {Z_L} = \sqrt 3 R{\rm{ }}\)
Khi mắc điện trở với tụ vào mạch thứ hai thì cường độ dòng điện là: \(I = \frac{{U'}}{{\sqrt {{R^2} + Z_C^2} }} = \frac{{2U}}{{2R}} = 1A\)
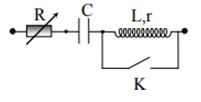
Cho mạch điện \(RLC\) không phân nhánh, cuộn dây có điện trở \(r\). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có tần số \(f{\rm{ }} = {\rm{ }}50Hz\). Cho điện dung \(C\) thay đổi người ta thu được đồ thị liên hệ giữa điện áp hai đầu phần mạch chứa cuộn dây và tụ điện như hình vẽ bên. Điện trở \(r\) có giá trị là:
-
A
\(80\Omega \)
-
B
\(100{\rm{ }}\Omega \)
-
C
\(50{\rm{ }}\Omega \)
-
D
\(60{\rm{ }}\Omega \)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính hiệu điện thế: \(U = IZ\)
+ Các trường hợp khi \(C\) biến thiên
+ Ta có biểu thức \({U_{rLC}} = \frac{{U\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{{\sqrt {{{\left( {r + R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
→ Tại C = 0 thì \({Z_C} = \infty \) , khi đó \({U_{rLC}} = U = 87V\)
→ Tại \(C = \infty \) thì \({Z_C} = 0\) , khi đó \({U_{rLC}} = \frac{{87\sqrt {{r^2} + Z_L^2} }}{{\sqrt {{{\left( {r + R} \right)}^2} + Z_L^2} }} = 36V\left( * \right)\)
+ Tại \(C = \frac{{100}}{\pi }\mu F \to {Z_C} = 100\Omega \) thì mạch xảy ra cộng hưởng \({Z_L} = {Z_C} = 100\Omega \) và \({U_{rLC}} = {U_{rLC\min }} = 17,4V\) \( \to {U_{rLC}} = \frac{{87r}}{{r + R}} = 17,4 \to R + r = 5r\)
→ Thay vào phương trình (*) ta tìm được \(r \approx 50\Omega \)
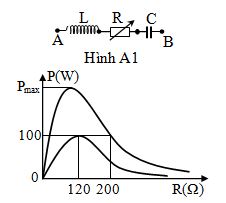
Cho mạch điện như hình A1, cuộn dây thuần cảm. Điện áp hai đầu đoạn mạch có biểu thức với \(U\) không đổi nhưng \(f\) có thể thay đổi được. Ta có đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ trên mạch theo \(R\) là đường liền nét khi \(f = {f_1}\) và là đường đứt nét khi \(f = {f_2}\) . Giá trị của \({P_{max}}\) gần nhất với giá trị nào sau đây?
-
A
\(280{\rm{ }}W\)
-
B
\(140{\rm{ }}W\)
-
C
\(130{\rm{ }}W\)
-
D
\(230{\rm{ }}W\)
Đáp án của giáo viên lời giải hay : C
+ Công suất cực đại khi mạch cộng hưởng: \(\omega = \frac{1}{{\sqrt {LC} }}\), khi đó: \({P_{max}} = \frac{{{U^2}}}{{2R}}\)
+ Bài toán \(f\) biến thiên có hai giá của \(R\) cho cùng một công suất: \(P = \frac{{{U^2}}}{{{Z^2}}}R \leftrightarrow P{R^2} - {U^2}R + {\left( {{Z_L} - {Z_C}} \right)^2}P = 0\)
+ Vận dụng định lí Vi-ét: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{{2a}}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\)
+ Ứng với tần số \({f_1}\) ta có công suất cực đại khi \({P_{max}} = \frac{{{U^2}}}{{2{R_0}}} = 100W\)
+ Ứng với tần số \({f_2}\) hai giá trị của \(R\) cho cùng một công suất là hai nghiệm của phương trình:\({P_{1m{\rm{ax}}}}{R^2} - {U^2}R + {({Z_L} - {Z_C})^2}{P_{1m{\rm{ax}}}} = 0\)
Theo định lý Vi-et ta có: \(\left\{ \begin{array}{l}{R_1} + {R_2} = \frac{{{U^2}}}{{{P_{1max}}}} = 2{R_0} \to {R_2} = 40\Omega \\{R_1}{R_2} = {({Z_L} - {Z_C})^2}\end{array} \right.\)
Công suất cực đại cần tìm: \({P_{max}} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2{R_0}}} \times \frac{{2{R_0}}}{{\sqrt {{R_1}{R_2}} }} = {P_{1max}}\frac{{{R_0}}}{{\sqrt {{R_1}{R_2}} }} \approx 134W\)
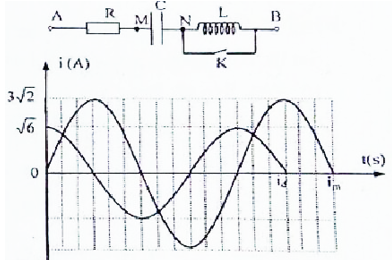
Cho mạch điện như hình vẽ, cuộn dây thuần cảm. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = 100\sqrt 6 \cos \left( {100\pi t + \varphi } \right)V\). Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là \({i_m}\) và \({i_d}\) được biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của \(R\) bằng:
-
A
\(50\Omega \)
-
B
\(100\sqrt 3 \Omega \)
-
C
\(100\Omega \)
-
D
\(50\sqrt 3 \Omega \)
Đáp án của giáo viên lời giải hay : A
Sử dụng kĩ năng đọc đồ thị và lí thuyết về đoạn mạch xoay chiều mắc nối tiếp
+ Từ đồ thị => viết phương trình cường độ dòng điện trong hai trường hợp: đóng và mở khóa K
+ Sử dụng công thức tính tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \frac{U}{I}\)
+ \({\varphi _1} + {\varphi _2} = \frac{\pi }{2} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\)
+ Sử dụng biểu thức: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Từ đồ thị ta thấy được biểu thức của cường độ dòng điện khi K đóng và mở là: \(\left\{ \begin{array}{l}{i_m} = 3\sqrt 2 \cos \left( {\omega t + \frac{\pi }{2}} \right)A\\{i_d} = \sqrt 6 \cos \left( {\omega t} \right)A\end{array} \right.\)
+ Khi khóa K đóng, mạch điện chỉ gồm R mắc nối tiếp với C
Tổng trở được tính theo công thức: \({Z_{RC}} = \sqrt {{R^2} + Z_C^2} {\rm{}} = \dfrac{{{U_0}}}{{{I_{01}}}} = \dfrac{{100\sqrt 6 }}{{\sqrt 6 }} = 100\Omega (1)\)
+ Khi khóa K mở, mạch điện gồm ba phần tử R, L, C mắc nối tiếp. Tổng trở được tính theo công thức \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} {\rm{}} = \dfrac{{{U_0}}}{{{I_{0m}}}} = \dfrac{{100\sqrt 6 }}{{3\sqrt 2 }} = \dfrac{{100\sqrt 3 }}{3}\Omega (2)\)
+ Từ biểu thức cường độ \({i_m}\) và \({i_d}\) ta thấy rằng hai dòng điện vuông pha với nhau, khi đó ta có: \(\dfrac{{{Z_C}}}{R}.\dfrac{{{Z_L} - {Z_C}}}{R} = 1 \Leftrightarrow {R^2} = {Z_C}\left( {{Z_L} - {Z_C}} \right)\left( 3 \right)\)
Thay (3) vào (1) và (2) ta được
\(\left\{ {\begin{array}{*{20}{l}}
{{Z_C}\left( {{Z_L} - {Z_C}} \right) + Z_C^2 = {{100}^2}} \\
{{Z_C}\left( {{Z_L} - {Z_C}} \right) + {{\left( {{Z_L} - {Z_C}} \right)}^2} = \dfrac{{{{100}^2}.3}}{9}}
\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{Z_L} = \dfrac{{200}}{{\sqrt 3 }}\Omega } \\
{{Z_C} = 50\sqrt 3 \Omega {\text{}}}
\end{array}} \right.\)
Thay vào (3) suy ra: \(R = 50\Omega \)
Cho mạch điện xoay chiều như hình vẽ. Điện dung \(C\) có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của \(C\) thì thấy: ở cùng thời điểm, số chỉ của \({V_1}\) cực đại (\({U_{A{M_{{\rm{max}}}}}}\)) thì số chỉ của \({V_1}\) gấp đôi số chỉ của \({V_2}\) . Hỏi khi số chỉ của \({V_2}\) cực đại ( \({U_{N{B_{{\rm{max}}}}}}\) ) thì số chỉ của \({V_2}\) gấp bao nhiêu lần số chỉ \({V_1}\)? (\({V_1}\) chỉ điện áp trên \(R\), còn \({V_2}\) chỉ điện áp trên \(C\))
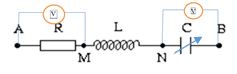
-
A
\(1,5\) lần
-
B
\(2\) lần
-
C
\(2,5\) lần
-
D
\(2\sqrt 2 \)lần
Đáp án của giáo viên lời giải hay : C
Áp dụng các tính toán đại số tìm điều kiện cực đại của điện áp khi tụ \(C\) thay đổi
+ C thay đổi để \({U_{{R_{{\rm{max}}}}}}\) khi đó mạch cộng hưởng
+ C thay đổi để \({U_{{C_{{\rm{max}}}}}}\) khi đó: \({U_{{C_{{\rm{max}}}}}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)
Khi \({V_1}\) đạt cực đại thì xảy ra cộng hưởng điện: \({U_{1\max }} = {U_R} = {U_{AB}}{\rm{ }} \Leftrightarrow {U_L} = {U_C}_1 = \frac{1}{2}{U_{AB}} = > R = 2{Z_L} = 2{Z_{C1}}\)
Thay đổi để điện áp trên tụ cực đại thì
\(\begin{array}{l}{U_{C\max }} = \frac{U}{R}.\sqrt {{R^2} + Z_L^2} khi{Z_C} = \frac{{{R^2} + Z_L^2}}{{{Z_L}}}\\I' = \frac{{{U_{C2}}}}{{{Z_{C2}}}} = \frac{{\frac{U}{R}.\sqrt {{R^2} + Z_L^2} }}{{\frac{{{R^2} + Z_L^2}}{{{Z_L}}}}} = \frac{{U.{Z_L}}}{{R.\sqrt {{R^2} + Z_L^2} }} = > {U_R}^\prime = I'.R = \frac{{U.{Z_L}}}{{\sqrt {{R^2} + Z_L^2} }} = \frac{U}{{\sqrt 5 }}V\\{U_{C\max }} = \frac{U}{R}.\sqrt {{R^2} + Z_L^2} = \frac{{U.\sqrt {4Z_L^2 + Z_L^2} }}{{2{Z_L}}} = \frac{{U.\sqrt 5 }}{2}V = > \frac{{{U_{C\max }}}}{{{U_R}^\prime }} = \frac{{\sqrt 5 }}{2}.\sqrt 5 = 2,5\end{array}\)
Đề thi THPT QG - 2020
Đặt điện áp xoay chiều u có giá trị hiệu dụng không đổi và tần số 50 Hz vào hai đầu đoạn mạch gồm điện trở \(30\Omega \) mắc nối tiếp với cuộn cảm thuần có độ tự cảm L thì cường độ dòng điện trong đoạn mạch là i. Hình bên là một phần đường cong biểu diễn mối liên hệ giữa i và p với \(p = ui\). Giá trị của L gần nhất với giá trị nào sau đây?
-
A
0,12 H
-
B
0,42 H
-
C
0,35 H
-
D
0,09 H
Đáp án của giáo viên lời giải hay : A
+ Đọc phương trình p-i
+ Sử dụng giản đồ
+ Sử dụng biểu thức tính độ lệch pha: \(\tan \varphi = \frac{{{Z_L}}}{R}\)
+ Sử dụng biểu thức tính cảm kháng: \({Z_L} = \omega L\)
+ Thời điểm \({t_1}\): \(i = 1 \Rightarrow p = ui = 1 \Rightarrow u = 1\)
+ Thời điểm \({t_2}\): \(i = 4 \Rightarrow p = ui = 4 = {p_{max}} \Rightarrow u = 1\)
Gọi \(\varphi \) là góc hợp bởi u; i
2 thời điểm \({t_1},{t_2}\) \({u_1} = {u_2}\) \( \Rightarrow \) trục \({t_1},{t_2}\) đối xứng nhau qua trục \({U_0}\), cùng hợp với \({U_0}\) một góc \(\alpha \)
+ Thời điểm \({t_2}\), \(p = ui\) và đạt cực đaij
\( \Rightarrow \) trục thời gian \({t_2}\) là phân giác của \(\left( {{U_0};{I_0}} \right)\) \( \Rightarrow \alpha = \frac{\varphi }{2}\)
Ta có: \(\left\{ \begin{array}{l}{i_1} = {I_0}cos\left( {\varphi + \alpha } \right) = {I_0}cos\left( {\frac{{3\varphi }}{2}} \right)\\{i_2} = {I_0}cos\left( {\varphi - \alpha } \right) = {I_0}cos\left( {\frac{\varphi }{2}} \right)\end{array} \right.\) \( \Rightarrow \frac{{{i_1}}}{{{i_2}}} = \frac{{cos\frac{{3\varphi }}{2}}}{{cos\frac{\varphi }{2}}} = \frac{1}{4} \Rightarrow \frac{\varphi }{2} = 0,448\left( {rad} \right)\)
Ta có: \(\tan \varphi = \frac{{{Z_L}}}{R} \Rightarrow {Z_L} = R.\tan \varphi \approx 37.496\Omega \)
Lại có: \({Z_L} = L\omega \Rightarrow L = \frac{{{Z_L}}}{\omega } = \frac{{37,496}}{{100\pi }} = 0,119H\)
