Đề bài
Cho đường tròn tâm O ngoại tiếp tam giác ABC. Số đo các góc A, B, C tương ứng là \({50^o},{60^o},{70^o}\). Từ O kẻ các đường thẳng OM, ON, OP lần lượt vuông góc với các dây BC, AC, AB tại M, N, P. So sánh các khoảng cách OM, ON và OP.
Phương pháp giải - Xem chi tiết
Sử dụng các định lí :
- Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
- Trong một đường tròn, dây lớn hơn thì gần tâm hơn.
Lời giải chi tiết
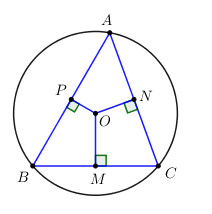
Ta có \(\widehat A < \widehat B < \widehat C\,\,\left( {{{50}^0} < {{60}^0} < {{70}^0}} \right)\) nên \(BC < AC < AB\) (trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn).
Do đó \(OM > ON > OP\) (trong một đường tròn, dây lớn hơn thì gần tâm hơn).
soanvan.me
