Đề bài
Cho bất phương trình bậc nhất hai ẩn: \(2x - 5y + 10 > 0\)
a) Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng Oxy
b) \(\left( {1;3} \right)\) có phải là nghiệm của bất phương trình trên không?
c) Chỉ ra 2 cặp số thỏa mãn bất phương trình trên
Phương pháp giải - Xem chi tiết
a) Bước 1: Vẽ đường thẳng của phương trình \(2x - 5y + 10 = 0\)
Bước 2: Xét 1 điểm bất kỳ thay vào bất phương trình và kết luận
b) Thay tọa độ điểm \(\left( {1;3} \right)\) vào bất phương trình và kiểm tra
c) Chọn x (hoặc y) bất kỳ và tìm ẩn còn lại thỏa mãn
Lời giải chi tiết
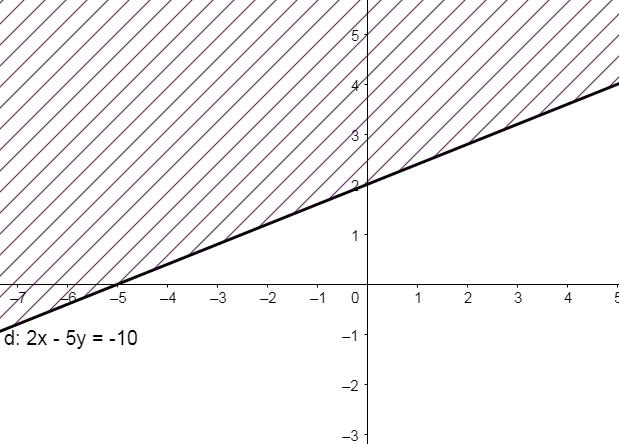
a) Vẽ đường thẳng \(d:2x - 5y + 10 = 0\) đi qua hai điểm \(A\left( {0;2} \right)\) và \(B\left( { - 5;0} \right)\)
Xét gốc tọa độ \(O\left( {0;0} \right)\)
Ta thấy \(O \notin d\) và \(2.0 - 5.0 + 10 = 10 > 0\). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ d, chứa gốc tọa độ O (miền không gạch chéo như hình dưới)
b) Thay tọa độ điểm \(\left( {1;3} \right)\) vào bất phương trình trên ta có:
\(2.1 - 5.3 + 10 = - 3 < 0\). Do đó \(\left( {1;3} \right)\) không là nghiệm của bất phương trình đã cho
c) Chọn \(x = 0 \Rightarrow 2.0 - 5y + 10 > 0 \Rightarrow y < 2\)
Vậy 2 cặp số thỏa mãn là nghiệm của bất phương trình đã cho là \(\left( {0;0} \right)\) và \(\left( {0;1} \right)\)
