Đề bài
Cho tam giác đều \(ABC\) cạnh bằng \(3cm\). Bán kính của đường tròn ngoại tiếp tam giác \(ABC\) bằng:
\((A)\,2\sqrt 3 \,cm;\)
\((B)\, 2cm;\)
\((C)\,\sqrt 3 \,cm;\)
\((D)\,\sqrt 2 \,cm;\)
Hãy chọn câu trả lời đúng.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất tam giác đều và tỉ số lượng giác của góc nhọn.
Cho tam giác \(ABC\) vuông tại \(A\) thì \(AB=BC.\sin \widehat C\)
Lời giải chi tiết
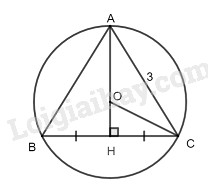
Vì \(O\) là tâm của đường tròn ngoại tiếp tam giác \(ABC\) nên \(O\) là giao điểm của ba đường trung trực trong tam giác \(ABC.\)
Kẻ \(AH \bot BC\), ta có: \(O \in AH\).
Trong tam giác vuông \(ABH\), ta có:
\(AH = AB.\sin \widehat B = 3.\sin 60^\circ = \dfrac{{3\sqrt 3 }}{ 2}\)
Vì tam giác \(ABC\) đều nên \(AH\) là đường cao cũng đồng thời là trung tuyến và O cũng là trọng tâm của tam giác ABC. Khi đó:
\(OA = \dfrac{2}{3}AH = \dfrac{2}{3}.\dfrac{{3\sqrt 3 }}{2} = \sqrt 3 \) cm.
Vậy bán kính của đường tròn ngoại tiếp tam giác \(ABC\) là: \(AO=\sqrt 3 \) cm.
Vậy chọn đáp án C.
soanvan.me
