Cho hàm số \(\displaystyle y = {{(2 + m)x + m - 1} \over {x + 1}}\)(1)
LG a
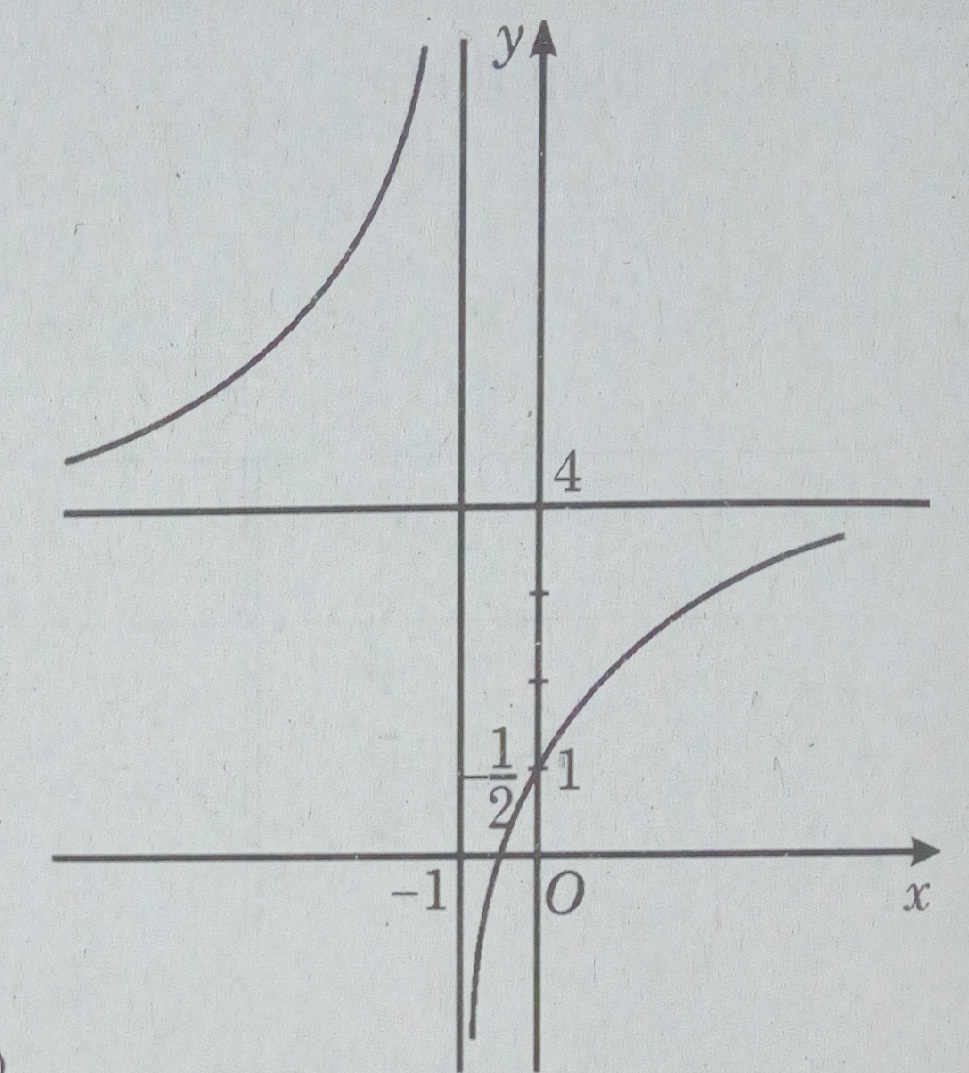
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2.
Lời giải chi tiết:
Với m = 2, ta có \(y = {{4x + 1} \over {x + 1}}\)
Đồ thị:
LG b
Xác định các điểm có tọa độ nguyên trên đồ thị của (1) khi \(m \in Z\).
Lời giải chi tiết:
Ta có \(y = 2 + m - {3 \over {x + 1}}\)
Vậy để y nguyên với x và m nguyên thì x + 1 phải là ước của 3, tức là: \(x + 1 = \pm 1\) hoặc \(x + 1 = \pm 3\) hay \({x_1} = 0;{x_2} = - 2;{x_3} = - 4;{x_4} = 2\) .
Vậy các điểm thuộc đồ thị của (1) có tọa độ nguyên là A(0; m -1) ; B(-2; 5 + m); C(-4; 3 + m); D(2; m + 1).
soanvan.me
