Đề bài
Trên mảnh đất có dạng hình chữ nhật với chiều dài là x (m), chiều rộng là y (m), người ta dự định làm một vườn hoa hình chữ nhật và bớt ra một phần đường đi rộng 2 m như ở Hình 2.
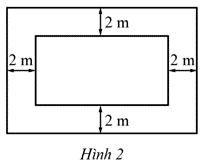
a) Viết biểu thức biểu thị chu vi và diện tích của vườn hoa trên mảnh đất đó
b) Tính chu vi và diện tích của vườn hoa trên mảnh đất đó, biết x = 15, y = 10
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn các kích thước của hình chữ nhật nhỏ theo x và y, sau đó tính diện tích hình chữ nhật nhỏ trong hình vẽ
Bước 2: Tìm biểu thức đại số biểu thị chu vi, diện tích phần đất còn lại (diện tích là hiệu của diện tích hình chữ nhật lớn và diện tích hình chữ nhật nhỏ)
Bước 3: Thay x = 15, y = 10 rồi tính giá trị các biểu thức trên
Lời giải chi tiết
a) Chiều dài hình chữ nhật nhỏ là: x – 2 – 2 = x – 4 (m)
Chiều rộng hình chữ nhật nhỏ là: y – 2 – 2 = y – 4 (m)
Vậy diện tích của vườn hoa trên mảnh đất đó là: \((x - 4)(y - 4)\) (m2)
Chu vi của vườn hoa trên mảnh đất đó là: \({\rm{[}}(x - 4) + (y - 4){\rm{]}}.2 = (x + y - 8).2 = 2(x + y - 8)\) (m)
b) Với x = 15, y = 10, chu vi của vườn hoa là: \(2(15 + 10 - 8) = 34\) (m)
Diện tích của vườn hoa là: \((15 - 4)(10 - 4) = 11.6 = 66\) (m2)
