Đề bài
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
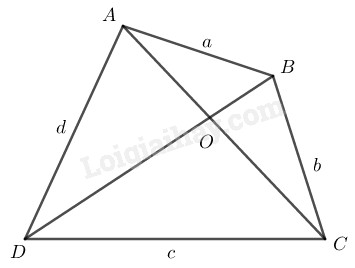
Đặt độ dài \(AB = a,\) \(BC = b,\) \( CD = c,\) \(AD = d\)
Gọi \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\)
Trong \(∆OAB,\) ta có:
\(OA + OB > a\) (bất đẳng thức tam giác)\( (1)\)
Trong \(∆OCD\) ta có:
\(OC + OD > c\) (bất đẳng thức tam giác)\( (2)\)
Từ \((1)\) và \((2)\) suy ra:
\(OA + OB + OC + OD > a + c\)
Hay \(AC + BD > a + c \;\;(*)\)
Trong \(∆OAD\) ta có: \(OA + OD > d\) (bất đẳng thức tam giác) \((3)\)
Trong \(∆OBC\) ta có: \(OB + OC > b\) (bất đẳng thức tam giác) \((4)\)
Từ \((3)\) và \((4)\) suy ra: \(OA + OD + OB + OC > b + d\)
\(⇒ AC + BD > b + d \;\;(**)\)
Từ \((*)\) và \((**)\) suy ra: \(2(AC + BD) > a + b + c + d\)
\(⇒ AC + BD > \displaystyle {{a + b + c + d} \over 2}\)
Trong \(∆ABC\) ta có: \(AC < AB + BC = a + b\) (bất đẳng thức tam giác)
Trong \(∆ADC\) ta có: \(AC < AD + DC = c + d\) (bất đẳng thức tam giác)
Suy ra: \(2AC < a + b + c + d\)
\(AC < \displaystyle {{a + b + c + d} \over 2}\) \((5)\)
Trong \(∆ABD\) ta có: \(BD < AB + AD = a + d\) (bất đẳng thức tam giác)
Trong \(∆BCD\) ta có: \(BD < BC + CD = b + c\) (bất đẳng thức tam giác)
Suy ra: \(2BD < a + b + c + d\)
\(BD < \displaystyle {{a + b + c + d} \over 2}\) \((6)\)
Từ \((5)\) và \((6)\) suy ra: \(AC + BD < a + b + c + d\)
Vậy \(\displaystyle {{a + b + c + d} \over 2}\)
soanvan.me
