Đề bài
Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:
a)\(\Delta MNC = \Delta BPM\)
b)\(\widehat {NMP} = {90^0}\)
Phương pháp giải - Xem chi tiết
a) \( \Delta MNC = \Delta BPM\left( {ch - gn} \right)\)
b) Chứng minh tứ giác MNAP là hình chữ nhật\(\widehat {MCN} = \widehat {BMP}\).
Lời giải chi tiết
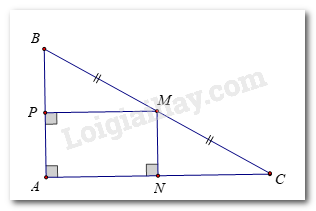
a)
Xét \(\Delta MNC\) và \(\Delta BPM\)có:
\(\begin{array}{l}\widehat {MNC} = \widehat {BPM} = {90^0}\\MC = BM\left( {gt} \right)\end{array}\)
\(\widehat {MCN} = \widehat {BMP}\)(cùng phụ với góc B)
\( \Rightarrow \Delta MNC = \Delta BPM\left( {ch - gn} \right)\)
b)
Xét tứ giác MNAP có:
\(\widehat A = \widehat {MPA} = \widehat {MNA} = {90^0}\)
\( \Rightarrow \)Tứ giác MNAP là hình chữ nhật
\( \Rightarrow \widehat {NMP} = {90^0}\)
