Đề bài
Cho góc nhọn \(xOy\) và điểm \(C\) nằm trong góc đó. Tìm trên \(Oy\) điểm \(A\) sao cho khoảng cách từ \(A\) đến \(Ox\) bằng \(AC\).
Phương pháp giải - Xem chi tiết
Để xác định một điểm \(M\) ta xem nó là ảnh của một điểm đã biết qua một phép vị tự.
Lời giải chi tiết
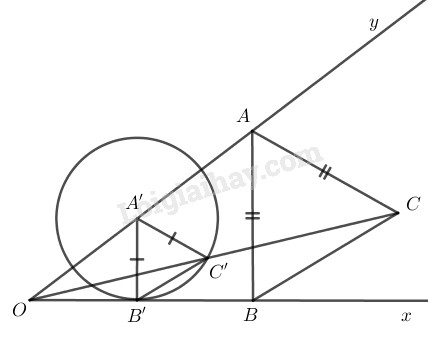
Giả sử điểm \(A\) đã dựng được . Gọi \(B\) là hình chiếu vuông góc của \(A\) trên \(Ox\), khi đó \(AB=AC\). Lấy điểm \(A’\) bất kì trên \(Oy\), gọi \(B’\) là hình chiếu vuông góc của \(A’\) trên \(Ox\), đường thẳng qua \(A'\) song song với \(AC\) cắt đường thẳng \(OC\) tại \(C’\). Khi đó có thể coi tam giác \(ABC\) là ảnh của tam giác \(A’B’C’\) qua phép vị tự tâm \(O\) tỉ số \(\dfrac{AC}{A’C’}\) nên \(A’C’=A’B’\).
Từ đó suy ra cách dựng:
- Lấy điểm \(A’\) bất kì trên \(Oy\), dựng \(B’\) là hình chiếu vuông góc của \(A’\) lên \(Ox\)
- Lấy \(C’\) là một giao điểm của đường tròn tâm \(A’\) bán kính \(A’B’\) với đường thẳng \(OC\).
- Đường thẳng qua \(C\) song song với \(A’C’\) cắt \(Oy\) tại \(A\).
Ta được \(A\) là điểm phải dựng.
soanvan.me
