Bài 1.40 trang 21 SBT giải tích 12

Đề bài

Hãy tìm tam giác vuông có diện tích lớn nhất nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số \(a\left( {a > 0} \right).\)

Lời giải chi tiết

Xét tam giác ABC vuông tại A như hình vẽ.

Gọi số đo cạnh góc vuông \(AB\) là \(x,0 < x < \dfrac{a}{2}\)

(vì \(AB < BC\) \( \Rightarrow 2AB < AB + BC = a\) \( \Rightarrow AB < \frac{a}{2}\))

Khi đó, cạnh huyền \(BC = a-x\), cạnh góc vuông còn lại là: \(AC = \sqrt {B{C^2} - A{B^2}} \) \( = \sqrt {{{(a - x)}^2} - {x^2}} \)

Hay \(AC = \sqrt {{a^2} - 2ax} \)

Diện tích tam giác \(ABC\) là: \(S(x) = \dfrac{1}{2}x\sqrt {{a^2} - 2ax} \)

\(S'(x) = \dfrac{1}{2}\sqrt {{a^2} - 2ax}  - \dfrac{1}{2}\dfrac{{ax}}{{\sqrt {{a^2} - 2ax} }}\)\( = \dfrac{{a(a - 3x)}}{{2\sqrt {{a^2} - 2ax} }}\)

\(S'(x) = 0 \Leftrightarrow x = \dfrac{a}{3}\)

Bảng biến thiên:

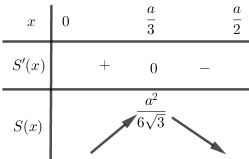
Tam giác có diện tích lớn nhất khi \(AB = \dfrac{a}{3};BC = \dfrac{{2a}}{3}\).

soanvan.me