Cho hàm số
\(y = {1 \over 3}{x^3} + (m - 1){x^2} + (2m - 3)x - {2 \over 3}\)
LG a
Với các giá trị nào của m, hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\)
Lời giải chi tiết:
\(y' = {x^2} + 2(m - 1)x + 2m - 3\)
\(y' = 0 \Leftrightarrow x = - 1,x = 3 - 2m\)
Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\) khi và chỉ khi
\(3 - 2m \le 1\)\( \Leftrightarrow m \le 1\)
Vậy \(m \ge 1\).
LG b
Với các giá trị nào của m, hàm số đồng biến trên R
Lời giải chi tiết:
Hàm số đồng biến trên R khi và chỉ khi
3 – 2m = -1 \( \Leftrightarrow m = 2\)
Vậy m=2.
LG c
Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m = 2
Lời giải chi tiết:
Với \(m = 2\) ta có: \(y = \frac{1}{3}{x^3} + {x^2} + x - \frac{2}{3}\)
+) TXĐ: \(D = \mathbb{R}\)
+) Chiều biến thiên:
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
\(y' = {x^2} + 2x + 1\) \( = {\left( {x + 1} \right)^2} \ge 0,\forall x \in \mathbb{R}\)
Hàm số đồng biến trên \(\mathbb{R}\) và không có cực trị.
BBT:
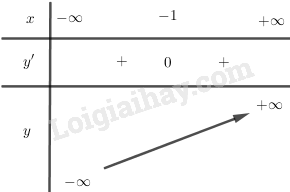
+) Đồ thị:
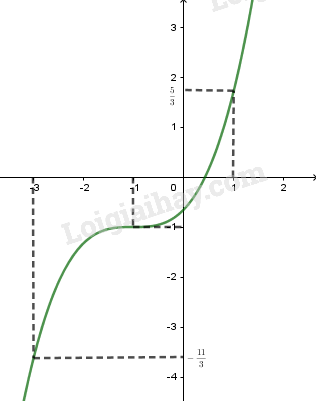
soanvan.me
