Đề bài
Một khung dây dẫn hình chữ nhật, kích thước 30 cm x 20 cm, được đặt trong một từ trường đều có phương vuông góc với mặt phẳng của khung dây và có cảm ứng từ là 0,10 T. Cho dòng điện cường độ 5,0 A chạy qua khung dây dẫn này. Xác định :
a) Lực từ tác dụng lên mỗi cạnh của khung dây'dẫn.
b) Lực từ tổng hợp tác dụng lên khung dây dẫn.
Phương pháp giải - Xem chi tiết
+ Sử dụng công thức tính lực từ: \(F = Bilsin\alpha\)
+ Sử dụng quy tắc bàn tay trái để xác định hướng của lực từ: Để bàn tay trái sao cho hướng của cảm ứng từ đi vào lòng bàn tay, chiều thừ cổ tay đến ngón tay chỉ chiều của dòng điện, ngón tay cái choãi ra \(90^0\) chỉ chiều của lực từ.
Lời giải chi tiết
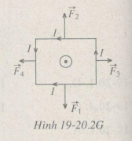
a) Áp dụng công thức \(F = Bilsin\alpha\) ( với \(α = \dfrac{π}{2}\), \(sinα =1\)) và quy tắc bàn tay trái để xác định độ lớn và hướng của lực từ tác dụng lên mỗi cạnh của khung dây dẫn (Hình 19-20.2G). Từ đó, ta suy ra :
- Lực từ tác dụng lên mỗi cạnh l1 = 30 cm :
\(\overrightarrow {{F_2}} = - \overrightarrow {{F_1}} \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow 0 \)
Có độ lớn:
\(F_1 =F_2 = BIl_1 = 0,10.5,0.0,30 = 0,15N.\)
- Lực từ tác dụng lên mỗi cạnh l2 = 20 cm :
\(\overrightarrow {{F_4}} = - \overrightarrow {{F_3}} \Rightarrow \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow 0 \)
Có độ lớn:
\(F_3 =F_4= BIl_2 = 0,10.5,0.0,20 = 0,10N.\)
b) Lực từ tổng hợp tác dụng lên khung dây dẫn có giá trị bằng :
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow 0 \)
(vì mỗi cặp lực từ tác dụng lên hai cạnh đối diện của khung dây dẫn có hợp lực bằng không \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow 0 \) và \(\overrightarrow {{F_3}} + \overrightarrow {{F_4}} = \overrightarrow 0 \) ).
soanvan.me