Đề bài
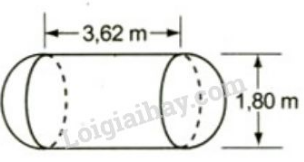
Một cái bồn chứa xăng gòm hai nửa hình cầu và một hình trụ (h.80). Hãy tính thể tích của bồn chứa xăng theo các kích thước cho trên hình vẽ.
Phương pháp giải - Xem chi tiết
+ Thể tích hình trụ bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h\)
+ Thể tích hình cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\)
Lời giải chi tiết
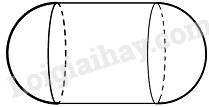
\(h = 3,62m\) ; \(d = 1,8m\) \( \Rightarrow R = 0,9m.\)
Gọi \(V,{V_T},{V_c}\) lần lượt là thể tích của bồn chứa xăng, hình trụ và hình cầu (gồm hai nửa hình cầu)
\({V_T} = \pi {r^2}h = {\rm{ }}\pi{\rm{ }}.{\left( {0,9} \right)^2}.3,62 \approx 9,21\left( {{m^3}} \right);\)
\({V_c} = \dfrac{4}{3}\pi {R^3} = \displaystyle {4 \over 3}.\pi.{(0,9)^3} \approx 3,05\,\left( {{m^3}} \right).\)
Vậy \(V = {V_T} + {V_c} = 9,21 + 3,05 = 12,26\)\(\left( {\,{m^3}} \right).\)
soanvan.me