Đề bài
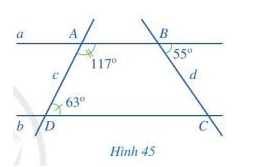
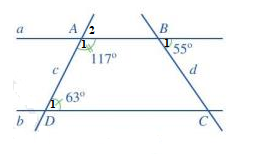
Quan sát Hình 45.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tính số đo góc BCD.
Phương pháp giải - Xem chi tiết
+ Sử dụng tính chất: Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong bằng nhau hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Sử dụng tính chất: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
Lời giải chi tiết
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) a // b (Dấu hiệu nhận biết hai đường thẳng song song) ( đpcm)
b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\) ( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ \Rightarrow \widehat {BCD} = 55^\circ \)