Đề bài
Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai \(f\left( x \right)\) với đồ thị được cho ở mỗi Hình 224a, 24b, 24c.
Phương pháp giải - Xem chi tiết
- Quan sát đồ thị và hoành độ giao điểm của đồ thị với trục hoành là nghiệm của phương trình \(f\left( x \right) = 0\).
- Lập bảng xét dấu cho mỗi hình.
Lời giải chi tiết
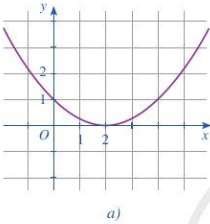
Hình 24a:
Ta thấy đồ thị cắt trục Ox tại điểm (2;0)
=> Phương trình \(f\left( x \right) = 0\) có nghiệm duy nhất \(x = 2\)
Ta thấy đồ thị nằm trên trục hoành nên có bảng xét dấu:
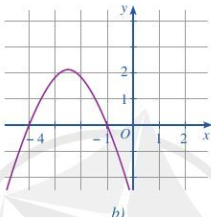
Hình 24b:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-4;0) và (-1;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 4,x = - 1\)
Trong các khoảng \(\left( { - \infty ; - 4} \right)\) và \(\left( { - 1; + \infty } \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Trong khoảng \(\left( { - 4; - 1} \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Bảng xét dấu:
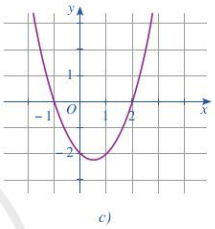
Hình 24c:
Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-1;0) và (2;0)
=> Phương trình \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = - 1,x = 2\)
Trong các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị nằm trên trục hoành nên \(f\left( x \right) > 0\)
Trong khoảng \(\left( { - 1;2} \right)\) thì đồ thị nằm dưới trục hoành nên \(f\left( x \right) < 0\)
Bảng xét dấu:
