Đề bài
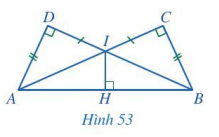
Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông. Chứng minh:
a) IA = IB;
b) IH là tia phân giác của góc AIB.
Phương pháp giải - Xem chi tiết
a) Chứng minh IA = IB, ta chứng minh tam giác IDA bằng tam giác ICB.
b) Một đường thẳng là đường vuông góc hạ từ một đỉnh của tam giác cân tại đỉnh đó thì đường thẳng đó là tia phân giác của tam giác đó.
Lời giải chi tiết
a) Xét tam giác IDA và tam giác ICB có:
ID = IC (gt), DA = CB (gt), \(\widehat D = \widehat C = 90^\circ \).
Vậy \(\Delta IDA = \Delta ICB\) (c.g.c)
\(\Rightarrow\) IA = IB (2 cạnh tương ứng)
b) Xét tam giác vuông IHA và tam giác vuông IHB có:
IH chung; IA = IB(gt)
Vậy \(\Delta IHA = \Delta IHB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow \widehat{AIH}=\widehat{BIH}\) ( 2 góc tương ứng)
Mà tia IH nằm trong góc AIB
\(\Rightarrow \) IH là tia phân giác của góc AIB.
