Đề bài
Trên hình \(103\) ta có hình thang \(ABCD\) với đường trung bình \(EF\) và hình chữ nhật \(GHIK.\) Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích hình chữ nhật có hai kích thước \(a,b\) là \(S=ab\)
- Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
$$S = {1 \over 2}\left( {a + b} \right).h$$
Lời giải chi tiết
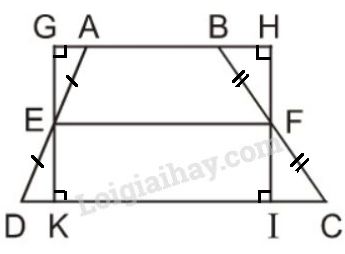
\(∆EKD\) và \(∆EGA\) có:
\(ED=EA\) (vì \(E\) là trung điểm \(AD\))
\( \widehat {DEK}=\widehat {A{\rm{E}}G} \) (đối đỉnh); \(\widehat {EKD} = \widehat {EGA} = {90^o}\)
Do đó \(∆EKD=∆EGA\) (cạnh huyền-góc nhọn)
suy ra \({S_{EKD}} = {S_{EGA}}\) (1)
Chứng minh tương tự \( S_{FIC}=S_{FHB}\) (2)
Từ (1) và (2) suy ra
\({S_{EKD}} + {S_{FIC}} = {S_{EGA}} + {S_{FHB}}\)
Cộng hai vế với \({S_{AEKIFB}}\) ta được
\({S_{ABCD}} = {S_{GHIK}}\)
Từ kết quả trên, ta suy ra diện tích hình thang bằng diện tích hình chữ nhật một cạnh bằng chiều cao của hình thang, cạnh kia bằng nửa tổng hai đáy của hình thang.
Do đó diện tích hình thang bằng nửa tổng hai đáy nhân với chiều cao. Đó là một cách khác chứng minh công thức diện tích hình thang.
soanvan.me
