Đề bài
Một hình nón tròn xoay có đỉnh là \(D\), tâm của đường tròn đáy là \(O\), đường sinh bằng \(l\) và có góc giữa đường sinh và mặt phẳng đáy bằng \(\alpha \).
a) Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
b) Gọi \(I\) là một điểm trên đường cao \(DO\) của hình nón sao cho \(\dfrac{{DI}}{{DO}} = k(0 < k < l)\). Tính diện tích thiết diện qua \(I\) và vuông góc với trục của hình nón.
Phương pháp giải - Xem chi tiết
a) Áp dụng các công thức: \({S_{xq}} = \pi rl\) và \(V = \dfrac{1}{3}\pi {r^2}h\).
b) Xác định tâm và bán kính của thiết diện (hình tròn), tính diện tích theo công thức \(S = \pi {R^2}\).
Lời giải chi tiết
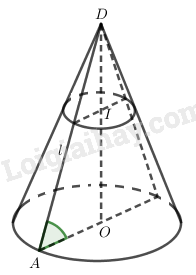
a) Gọi \(r \) là bán kính của đường tròn đáy.
Ta có \(OA{\rm{ }} = {\rm{ }}r{\rm{ }} = l.\cos \alpha \) (với \(O\) là tâm của đường tròn đáy và \(A\) là một điểm trên đường tròn đó).
Ta suy ra: \({S_{xq}} = \pi rl = \pi {l^2}\cos \alpha \)
Khối nón có chiều cao \(h = DO = l\sin \alpha \). Do đó thể tích \(V\) của khối nón được tính theo công thức \(V = \dfrac{1}{3}Bh = \dfrac{1}{3}\pi {r^2}.h\)
Vậy : \(V = \dfrac{1}{3}\pi {l^2}{\cos ^2}\alpha .l\sin \alpha = \dfrac{1}{3}\pi {l^3}{\cos ^2}\alpha \sin \alpha \)
b) Thiết diện qua \(I\) và vuông góc với trục hình nón là một hình tròn bán kính \(r’\) với \(\dfrac{{r'}}{r} = \dfrac{{DI}}{{DO}} = k\)\( \Rightarrow r' = kr = k.l\cos \alpha \).
Vậy diện tích của thiết diện đi qua điểm \(I\) và vuông góc với trục hình nón là: \(S = \pi r{'^2} = \pi {k^2}{l^2}{\cos ^2}\alpha \)
soanvan.me
