Cho hình chóp \(S.ABCD\) có đáy là hình hình hành \(ABCD\). Tìm giao tuyến của các cặp mặt phẳng sau đây:
LG a
\((SAC)\) và \((SBD)\)
Phương pháp giải:
Muốn tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng.
Lời giải chi tiết:
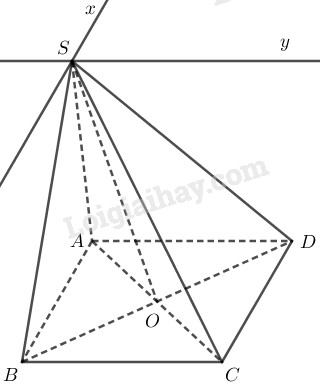
Ta có: \(S\in (SAC)\cap(SBD)\)
Gọi \(AC \cap BD = O\)
Mà \(AC\subset (SAC)\), \(BD\subset (SBD)\) \(\Rightarrow O\in (SAC)\cap(SBD)\)
\(\Rightarrow (SAC) \cap (SBD) = SO\).
LG b
\((SAB)\) và \((SCD)\)
Phương pháp giải:
Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng \(d\) và \(d’\) song song với nhau:
- Tìm điểm chung của hai mặt phẳng
- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với \(d\) và \(d’\).
Lời giải chi tiết:
Ta có: \(S\in (SAB)\cap(SCD)\)
Ta lại có:
\(\left\{ \begin{array}{l}AB \subset (SAB)\\CD \subset (SCD)\\AB\parallel CD\end{array} \right.\)
\(\Rightarrow (SAB)\cap (SCD)=Sx,\)
\(Sx\parallel AB\parallel CD\).
LG c
\((SAD)\) và \((SBC)\).
Phương pháp giải:
Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng \(d\) và \(d’\) song song với nhau:
- Tìm điểm chung của hai mặt phẳng
- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với \(d\) và \(d’\).
Lời giải chi tiết:
Ta có: \(S\in (SAD)\cap(SBC)\)
Ta lại có:
\(\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD\parallel BC\end{array} \right.\)
\(\Rightarrow (SAD)\cap (SBC)=Sy,\)
\(Sy\parallel AD\parallel BC\).
soanvan.me
