Đề bài
Cho tam giác cân \(ABC\) \((AB = AC)\) nội tiếp đường tròn tâm \(O.\) Các đường phân giác của hai góc \(B\) và \(C\) cắt nhau ở \(E\) và cắt đường tròn lần lượt ở \(F\) và \(D.\) Chứng minh rằng tứ giác \(EDAF\) là một hình thoi.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc kề cạnh đáy bằng nhau.
+) Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
+) Tứ giác có các cặp góc song song là hình bình hành.
+) Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Lời giải chi tiết
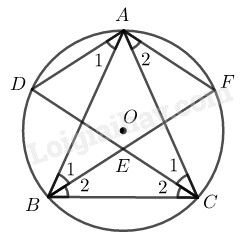
Vì \(∆ABC\) cân tại \(A\)
\( \Rightarrow \widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Lại có:
\(BF\) là tia phân giác của \(\widehat {ABC}\) \((gt)\)
\(CD\) là tia phân giác của \(\widehat {ACB}\) \((gt)\)
Suy ra: \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra: \(\overparen{AD}\)\(=\overparen{DB}\)\(=\overparen{AF}\)\(=\overparen{FC}\)
Từ đó, đường tròn \((O)\) có: \(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc nội tiếp chắn \(2\) cung bằng nhau \(BD\) và \(AF\))
\( \Rightarrow AD//BF\) (vì có cặp góc so le trong bằng nhau)
Hay \(AD // EF\;\;\; (1)\)
Tương tự: \(\widehat {{A_2}} = \widehat {{C_1}}\) (hai góc nội tiếp chắn \(2\) cung bằng nhau)
\( \Rightarrow AF // CD\) (vì có cặp góc ở vị trí so le trong bằng nhau)
Hay \(AF // ED \;\;\; (2)\)
Mà \(\overparen{AD}= \overparen{AF}\) (chứng minh trên)
\( \Rightarrow AD = AF\) \( (3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: Tứ giác \(ADEF\) là hình thoi
soanvan.me
