Bài 2.50 trang 84 SBT hình học 11

Đề bài

Cho tứ diện \(ABCD\). Tìm vị trí điểm \(M\) trong không gian sao cho: \(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị cực tiểu.

Lời giải chi tiết

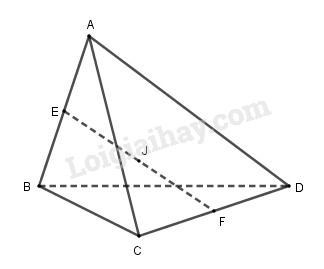
Gọi \(\displaystyle E, F\) lần lượt là trung điểm của \(\displaystyle AB\) và \(\displaystyle CD\). Ta có:

\(\begin{array}{l}
M{A^2} + M{B^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2}\\
= {\left( {\overrightarrow {ME} + \overrightarrow {EA} } \right)^2} + {\left( {\overrightarrow {ME} + \overrightarrow {EB} } \right)^2}\\
= {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EA} + {\overrightarrow {EA} ^2}\\
+ {\overrightarrow {ME} ^2} + 2\overrightarrow {ME} .\overrightarrow {EB} + {\overrightarrow {EB} ^2}\\
= 2M{E^2} + 2\overrightarrow {ME} \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + E{A^2} + E{B^2}\\
= 2M{E^2} + 0 + \frac{1}{4}A{B^2} + \frac{1}{4}A{B^2}\\
= 2M{E^2} + \frac{1}{2}A{B^2}
\end{array}\)

Do đó, \(\displaystyle M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right)\)

\(\displaystyle M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)

Cộng (1) và (2) ta có:

\(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\)

\(\displaystyle = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)

Gọi \(\displaystyle J\) là trung điểm của \(\displaystyle EF\), ta có:

\(\displaystyle \left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)

Khi đó:

\(\displaystyle \eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr 
& = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr 
&  = 4M{J^2} + E{F^2} + \frac{1}{2}\left( {A{B^2} + C{D^2}} \right)\cr &\ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)

Vậy \(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(MJ = 0\) hay \(\displaystyle M \equiv J\).

soanvan.me