Đề bài
Lăng kính có chiết suất n và góc chiết quang A. Một tia sáng đơn sắc được chiếu tới lăng kính sát mặt trước. Tia sáng khúc xạ vào lăng kính và ló ra ớ mặt kia với góc ló i’. Chứng minh hệ thức
\(\dfrac{{{\rm{cosA + sini'}}}}{{\sin A}} = \sqrt {{n^2} - 1} \)
Phương pháp giải - Xem chi tiết
Sử dụng công thức lăng kính :\( A= r_1 + r_2\) ; \( sini=nsinr\)
Lời giải chi tiết
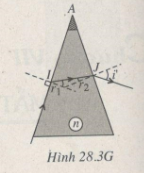
Ta có ở I (Hình 28.3G):
nsinr1 = sin900 --> \(sinr_1 = \dfrac{1}{n}\)
Mặt khác: \(r_1+r_2 = A => r_2 = A -r_1\)
Ở J:
\(\begin{array}{l}
n\sin {r_2} = \sin i'\\
\Rightarrow n\sin (A - {r_1}) = \sin i'\\
\Rightarrow \sin A\cos {r_1} - {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}{\rm{cosA = }}\dfrac{{\sin i'}}{n}\\
\Rightarrow \sin A\sqrt {1 - {{\sin }^2}_{{r_1}}} - {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_1}{\rm{cosA = }}\dfrac{{\sin i'}}{n}\\
\Rightarrow \sin A\dfrac{{\sqrt {{n^2} - 1} }}{n} - \dfrac{{{\rm{cosA}}}}{n} = \dfrac{{\sin i'}}{n}
\end{array}\)
Do đó: \(\dfrac{{{\rm{cosA + sini'}}}}{{\sin A}} = \sqrt {{n^2} - 1} \)