Đề bài
Một thấu kính hội tụ có tiêu cự f = 20cm. Tìm vị trí của vật trước thấu kính để ảnh của vật tạo bởi thấu kính gấp 4 lần vật.
Giải bài toán bằng hai phương pháp:
a) Tính toán.
b) Vẽ.
Phương pháp giải - Xem chi tiết
Sử dụng biểu thức tính : \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
Lời giải chi tiết
a) Giải bằng tính toán
Vật thật có thể có ảnh thật hoặc ảnh ảo qua thấu kính hội tụ
* Ảnh thật:
\({k_1} = \dfrac{f}{{f - d}} = - 4 \Rightarrow d = \dfrac{{5f}}{4} = \dfrac{{5.20}}{4} = 25cm\)
* Ảnh ảo:
\({k_2} = \dfrac{f}{{f - d}} = 4 \Rightarrow d = \dfrac{{3f}}{4} = \dfrac{{3.20}}{4} = 15cm\)
b) Giải bằng phép vẽ:
* Ảnh thật:
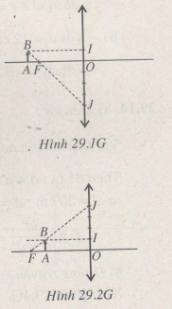
Ảnh ngược chiều so với vật và bằng 4 lần vật (Hình 29.1G)
- Lấy trên thấu kính \(\overline {{\rm{OJ}}} = - 4\overline {OI} \)
- Kẻ đường thẳng qua I song song với trục chính.
- Nối JF cắt đường thẳng trên tại B.
- Hạ BA vuông góc với trục chính.
AB là vị trí vật.
Tính đồng dạng cho:
FA = 5cm à OA = 25cm
* Ảnh ảo:
Ảnh cùng chiều so với vật. Thực hiện cách vẽ tương tự (HÌnh 29.2G) nhưng với \(\overline {{\rm{OJ}}} = 4\overline {OI} \)
Ta có FA = 5cm; \(OA = 20 – 5 = 15cm.\)
soanvan.me