Đề bài
Một bãi đậu xe ban đêm có diện tích đậu xe là 150 m2 (không tính lối đi cho xe ra vào). Cho biết xe du lịch cần diện tích 3 m2/chiếc và phải trả phí 40 nghìn đồng, xe tải cần diện tích 5 m2/chiếc và phải trả phí 50 nghìn đồng. Nhân viên quản lí không thể phục vụ quá 40 xe một đêm. Hãy tính số lượng xe mỗi loại mà chủ bãi xe có thể đăng kí đậu xe để có doanh thu cao nhất
Lời giải chi tiết
Gọi x,y là số xe du lịch và xe tải đậu xe ở bãi.
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
\(\left\{ \begin{array}{l}3x + 5y \le 150\\x + y \le 40\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn miền nghiệm của hệ phương trình trên hệ trục tọa độ Oxy ta được miền nghiệm đa giác OABC.
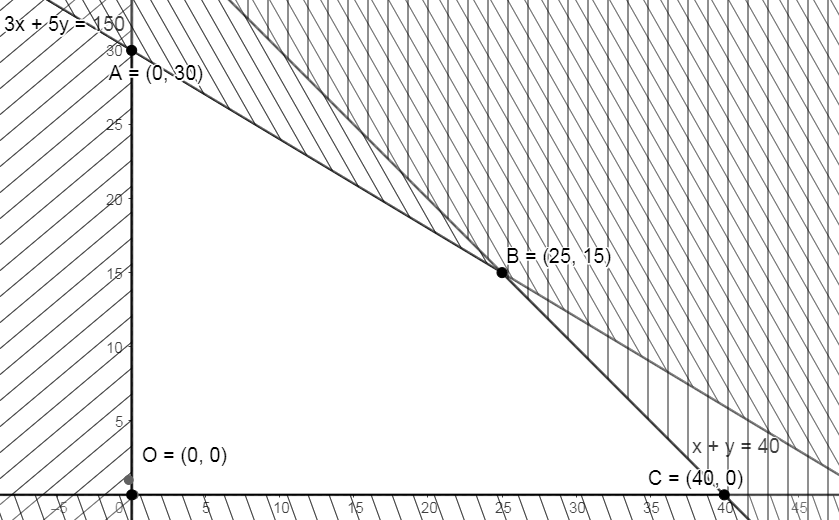
Tọa độ các đỉnh của đa giác đó là: \(O\left( {0;0} \right),A\left( {0;30} \right),B\left( {25;15} \right),C\left( {40;0} \right)\)
Gọi F là doanh thu (đơn vị: nghìn đồng) chủ bãi xe thu được, ta có: \(F = 40x + 50y\)
Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F lớn nhất, nghĩa là tìm giá trị lớn nhất của \(F = 40x + 50y\) trên miền đa giác OABC
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại \(0\left( {0;0} \right)\): \(F = 40.0 + 50.0 = 0\)
Tại A (0; 30): \(F = 40.0 + 50.30 = 1500\)
Tại B (25; 15): \(F = 40.25 + 50.15 = 1750\)
Tại C (40; 0): \(F = 40.40 + 50.0 = 1600\)
Vậy ta thấy tại đỉnh B (25; 15) thì giá trị F lớn nhất
Vậy chủ bãi xe có thể đăng kí 25 xe du lịch và 2 xe khách mỗi đêm để có doanh thu lớn nhất là 1750 nghìn đồng
