Đề bài
Cho hai điểm A, B là vị trí của hai nhà máy cùng về mpptj phía bờ sông là đường thẩng a. Vẽ điểm C sao cho a là đường trung trực của AC. Lấy điểm M tùy yá trên a.
a) Chứng minh MA + MB \( \ge \) BC
b) Tìm vị trí của địa điểm \({M_o}\) trên bờ sông để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất
Phương pháp giải - Xem chi tiết
- Sử dụng với điểm M, B, C tùy ý ta luôn có: MB + MC \( \ge \) BC để suy ra điều chứng minh ở bài toán và tìm vị trí \({M_o}\)
Lời giải chi tiết
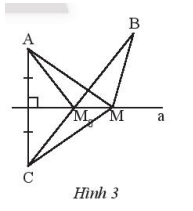
a) Ta có điểm M nàm trên trung trực của AC, suy ra MA = MC.
Với ba điểm tùy ý M, B, C ta luôn có:
\(MB + MC \ge BC\)
Vậy \(MA + MB \ge BC\)
b) Ta có: \(MA + MB \ge BC\), suy ra MA + MB ngắn nhất khi B< C, M thẳng hàng.
Vậy điểm \({M_o}\), cần tìm là giao điểm của đường thẳng BC và đường thẳng a.
