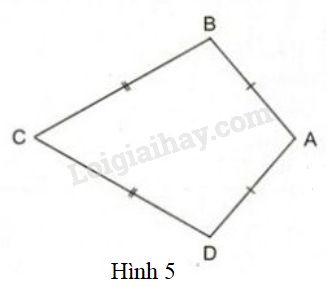
Ta gọi tứ giác \(ABCD\) trên hình \(5\) có \(AB = AD, CB = CD\) là hình "cái diều"
LG a
Chứng minh rằng \(AC\) là đường trung trực của \(BD.\)
Phương pháp giải:
Áp dụng:
- Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
- Định lý: Tổng các góc của một tứ giác bằng \({360^0}\)
- Tính chất hai tam giác bằng nhau.
Giải chi tiết:
\(AB = AD\) nên \( A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) nên \( C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD.\)
LG b
Tính \(\widehat B;\widehat D\) biết rằng \(\widehat A = {100^0};\widehat C = {60^0}\).
Phương pháp giải:
Áp dụng:
- Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
- Định lý: Tổng các góc của một tứ giác bằng \({360^0}\)
- Tính chất hai tam giác bằng nhau.
Giải chi tiết:

\(∆ ABC = ∆ADC\) (c.c.c) suy ra \(\widehat B = \widehat D\) (hai góc tương ứng)
Ta lại có: \(\widehat B + \widehat {{D}} ={360^0} - {{{60}^0} - {100}^0} = {200^0}\)
Do đó \(\widehat B= {100^0} ;\; \widehat {D} = {100^0} \) (vì \(\widehat B = \widehat D)\)
Giải thích:
Xét \(∆ ABC\) và \(∆ADC\) có:
+) \(AB = AD\) (giả thiết)
+) \(BC = DC\) (giả thiết)
+) \(AC\) cạnh chung
\( \Rightarrow ∆ ABC = ∆ADC\) (c.c.c)
soanvan.me
