Bài 30 trang 75 - Sách giáo khoa toán 8 tập 2

Đề bài

Tam giác \(ABC\) có độ dài các cạnh là \(AB = 3cm, AC = 5cm, BC = 7cm\). Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) và có chu vi bằng \(55 cm\). 

Hãy tính độ dài các cạnh của \(A'B'C'\) (làm tròn đến chữ số thập phân thứ hai).

Lời giải chi tiết

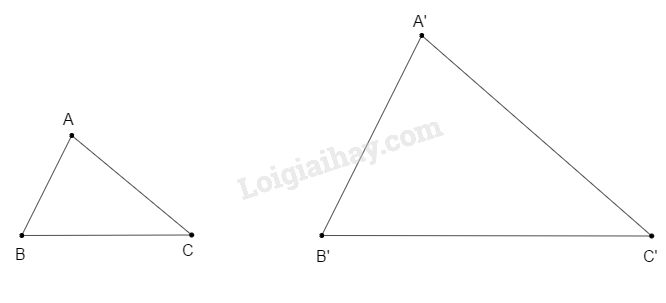
\( \Rightarrow \Delta ABC \) đồng dạng \( \Delta A'B'C'\left( {gt} \right)\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}\)\(\, = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}\) \( = \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}}\)

hay \(\dfrac{3}{A'B'}\) = \(\dfrac{7}{B'C'}\) = \(\dfrac{5}{A'C'}\) = \(\dfrac{C_{ABC}}{55}\) = \(\dfrac{3 + 7 + 5}{55}\) = \(\dfrac{{15}}{{55}}\) = \(\dfrac{3}{11}\)

(với \(C_{ABC}\) và \(C_{A'B'C'}\) lần lượt là chu vi của hai tam giác \(ABC, A'B'C'\))  

\( + )\,\,\dfrac{3}{{A'B'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow A'B' = \dfrac{{3.11}}{3} = 11\,cm\) 

\( + )\,\,\dfrac{7}{{B'C'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow B'C' = \dfrac{{7.11}}{3} \approx  25,67\,cm\)

\( + )\,\,\dfrac{5}{{A'C'}} = \dfrac{3}{{11}}\)\(\; \Rightarrow A'C' = \dfrac{{5.11}}{3} \approx 18,33\,cm\) 

soanvan.me