Bài 30.9 trang 85 SBT Vật lý 11

Đề bài

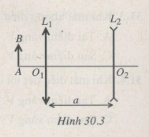
Cho hệ quang học như Hình 30.3 : f₁ = 30 cm ; f₂ = -10 cm ; O₁O₂ = a.

a) Cho AO₁ = 36 cm, hãy :

- Xác định ảnh cuối cùng A'B' của AB tạo bởi hệ với a = 70 cm.

- Tìm giá trị của a để A'B' là ảnh thật.

b) Với giá trị nào của a thì số phóng đại ảnh cuối cùng A'B' tạo bởi hệ thấu kính không phụ thuộc vào vị trí của vật?

Lời giải chi tiết

\(\begin{array}{l}
AB-->{A_1}{B_1}-->A'B'\\
{d_1} = 36cm;{d_1}' = \dfrac{{36.30}}{{36 - 30}} = 180cm\\
{d_2} = a - {d_1}' = - 110cm;{d_2}' = \dfrac{{( - 110)( - 10)}}{{ - 110 + 10}} = - 11cm
\end{array}\)

Ảnh ảo  cách O₂ 11cm.

\(k = {k_1}{k_2} = \left( { - \dfrac{{{d_1}'}}{{{d_1}}}} \right)\left( { - \dfrac{{{d_2}'}}{{{d_2}}}} \right) = \dfrac{{180}}{{36}}.\dfrac{{11}}{{110}} = \dfrac{1}{2}\)

Ảnh cùng chiều và bằng nửa vật.

* Muốn có A’B’ thật thì:

f₂ < d₂ < 0 --> d₂ = a – 180

Do đó:

            a – 180 < 0 --> a < 180cm

            a – 180 > -10 --> a > 170cm

Hay 170cm < a < 180cm

b) k = k₁k₂ nhưng   \({k_1} = \dfrac{{{f_1}}}{{{f_1} - d}};{k_2} = \dfrac{{{f_2}}}{{{f_2} - {d_2}}}\)

Mà:

\(\begin{array}{l}
{d_2} = a - {d_1}' = a - \dfrac{{{d_1}{f_1}}}{{{d_1} - {f_1}}} = \dfrac{{(a - {f_1}){d_1}{\rm{ - a}}{{\rm{f}}_1}}}{{{d_1} - {f_1}}}\\
{f_2} - {d_2} = {f_2} - \dfrac{{(a - {f_1}){d_1}{\rm{ - a}}{{\rm{f}}_1}}}{{{d_1} - {f_1}}} = \dfrac{{({f_2} + {f_1} - a){d_1} + a{f_1} - {f_1}{f_2}}}{{{d_1} - {f_1}}}\\
{k_2} = \dfrac{{{f_2}({d_1} - {f_1})}}{{({f_2} + {f_1} - a){d_1} + a{f_1} - {f_1}{f_2}}}
\end{array}\)

Vậy  

\(k = \dfrac{{{f_1}{f_2}}}{{{f_1}{f_2} - a{f_1} - ({f_2} + {f_1} - a){d_1}}}\)

Muốn k không phụ thuộc vào d₁ ta phải có:

            f₂ + f₁ – a = 0  => a = f₁ + f₂ (tức F₁’ ≡ F₂)

Chú ý: Có thể giải bằng phương pháp hình học, dùng hai tia sang tương ứng song song với trục chính.

soanvan.me