Đề bài
Cho đường thẳng xx’, điểm A thuộc xx’. Trên tia Ax’ lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm M. Hai điểm N và P thoả mãn \(\widehat {NMA} = \widehat {MAB};\widehat {PMy} = \widehat {MBx'}\) (H.3.21). Giải thích tại sao ba điểm N, M, P thẳng hàng.
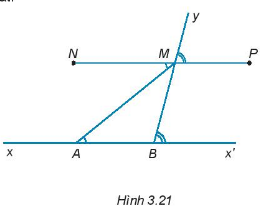
Phương pháp giải - Xem chi tiết
- Chứng minh: \(MN\parallel xx'\),\(MP\parallel xx'\)
- Áp dụng tiên đề Euclid.
Lời giải chi tiết
Ta có: \(\widehat {NMA} = \widehat {MAB}\), mà hai góc này ở vị trí so le trong, suy ra \(MN\parallel xx'\)
\(\widehat {PMy} = \widehat {MBx'}\), mà hai góc này ở vị trí đồng vị, suy ra \(MP\parallel xx'\)
Theo tiên đề Euclid, qua điểm M chỉ có một đường thẳng song song với xx’.
Do đó hai đường thẳng MN và MP trùng nhau
Suy ra N, M, P thẳng hàng
