Đề bài
Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Phương pháp giải - Xem chi tiết
Sử dụng: +Tính chất của hình thang: 2 cạnh đáy song song.
+Tính chất 2 đường thẳng song song
Lời giải chi tiết
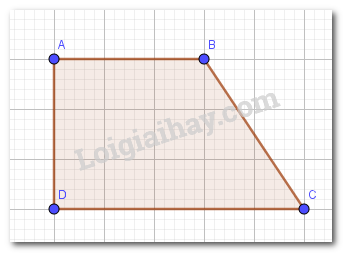
Vì AD vuông góc với hai đáy AB và CD nên \(\widehat{A}=\widehat{D}=90^0\)
Vì ABCD có 2 đáy AB,CD nên AB // CD. Do đó, \(\widehat B + \widehat C = 180^\circ \) ( 2 góc trong cùng phía)
Mặt khác:
\(\begin{array}{l}\widehat B = 2.\widehat C\\ \Rightarrow 2.\widehat C + \widehat C = 180^\circ \\ \Rightarrow 3.\widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ :3 = 60^\circ \end{array}\)
\(\Rightarrow \widehat B = 2. \widehat{C}=2.60^0=120^0\)
Vậy \(\widehat{A}=\widehat{D}=90^0; \widehat B = 120^0; \widehat C =60^0\)
