Đề bài
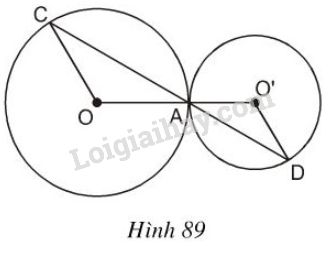
Trên hình 89 hai đường tròn tiếp xúc nhau tại \(A\). Chứng minh rằng \(OC//O'D\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm. Tức là nếu \((O)\) và \((O')\) tiếp xúc nhau tại \(A\) thì \(O,\ A,\ O'\) thẳng hàng.
+) Nếu \(A,\ B\) thuộc \((O;\ R)\) thì \(OB=OA=R\)
Lời giải chi tiết
Vì \((O)\) và \((O’)\) tiếp xúc nhau tại \(A\) (gt) ⇒ \(O,\ A,\ O’\) thẳng hàng nên \(\widehat {OAC} = \widehat {O'{\rm{AD}}}\) (đối đỉnh) (1)
Xét \(\Delta{OCA}\) có \(OC = OA\) (= bán kính (O)) nên tam giác OCA cân tại \(O\).
\( \Rightarrow \widehat {OAC} = \widehat {OC{\rm{A}}}\) (2)
Xét tam giác \(O'AD\) có O'A=O'D= bán kính (O')) nên cân tại \(O'\)
\( \Rightarrow \widehat {O'A{\rm{D}}} = \widehat {O'DA}\) (3)
Từ (1), (2) và (3)\( \Rightarrow \widehat {OC{\rm{A}}} = \widehat {O'DA}\)
Mà 2 góc này ở vị trí so le trong
\( \Rightarrow OC // O’D\) (đpcm)
