Bài 3.30 trang 151 SBT hình học 11

Đề bài

Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh  B và , có cạnh SA vuông góc với mặt phẳng (ABC) và SA = a.

a) Chứng minh mặt phẳng (SAB) vuông góc với  mặt phẳng (SBC).

b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh \(AH \bot \left( {SBC} \right)\)

c) Tính độ dài đoạn AH.

d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK.

Lời giải chi tiết

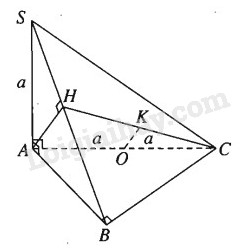
a)

\(\displaystyle \left. \matrix{
BC \bot AB \hfill \cr 
BC \bot SA \hfill \cr} \right\} \Rightarrow BC \bot \left( {SAB} \right) \) \(\displaystyle \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)

b) \(\displaystyle AH \bot SB\) mà SB giao tuyến của hai  mặt phẳng vuông góc là (SBC) và (SAB) nên \(\displaystyle AH \bot \left( {SBC} \right)\).

c) Xét tam giác vuông SAB với đường cao AH  ta có:

\(\displaystyle {1 \over {A{H^2}}} = {1 \over {A{S^2}}} + {1 \over {A{B^2}}} \) \(\displaystyle = {1 \over {{a^2}}} + {1 \over {2{a^2}}} = {3 \over {2{a^2}}}\)

Vậy \(\displaystyle AH = {{a\sqrt 6 } \over 3}\)

d) Vì \(\displaystyle OK \bot \left( {SBC} \right)\) mà \(\displaystyle AH \bot \left( {SBC} \right)\) nên \(\displaystyle OK\parallel AH\), ta có K thuộc CH.

\(\displaystyle OK = {{AH} \over 2} = {{a\sqrt 6 } \over 6}\).

 soanvan.me