Đề bài
Cho góc vuông uOv và tia Oy đi qua một điểm trong của góc đó. Vẽ tia Ox sao cho Ou là tia phân giác của góc xOy. Vẽ tia Oz sao cho Ov là tia phân giác của góc yOz. Chứng minh rằng hai góc xOy và yOz là hai góc kề bù.
Phương pháp giải - Xem chi tiết
- Biểu diễn hai góc xOy theo góc uOy, góc yOz theo góc yOv.
- Chứng minh tổng hai góc xOy và yOz bằng 180 độ.
Lời giải chi tiết
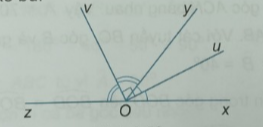
Vì tia Ou là tia phân giác của góc xOy; Ov là tia phân giác của góc yOz nên:
\(\begin{array}{l}\widehat {xOy} = 2\widehat {uOy},\widehat {yOz} = 2\widehat {yOv}\\ \Rightarrow \widehat {xOy} + \widehat {yOz} = 2\left( {\widehat {uOy} + \widehat {yOv}} \right) = {2.90^0} = {180^0}\end{array}\)
Mà 2 góc này kề nhau.
Vậy hai góc xOy và yOz là hai góc kề bù.
