Đề bài
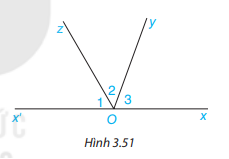
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau
a) Tính tổng số đo ba góc O1, O2, O3 .
Gợi ý: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong đó \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)
b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_2}} = 70^\circ \). Tính \(\widehat {{O_2}}\)
Phương pháp giải - Xem chi tiết
2 góc kề bù có tổng số đo là 180 độ
Lời giải chi tiết
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)
