Bài 33.7 trang 92 SBT Vật lý 11

Đề bài

Vật kính và thị kính của một kính hiển vi có tiêu cự lần lượt là f₁ = l cm; f₂  = 4 cm. Độ dài quang học của kính là d= 15 cm.

Người quan sát có điểm C_c cách mắt 20 cm và điểm C_v ở vô cực.

a) Hỏi phải đặt vật trong khoảng nào trước kính (mắt đặt sát kính) ?

b) Năng suất phân li của mắt người quan sát là ε = 1'. Tính khoảng cách nhỏ nhất giữa hai điểm của vật mà người quan sát còn phân biệt được khi ngắm chừng ở vô cực. 

Lời giải chi tiết

a) Khoảng có thể xê dịch vật MN tương ứng với khoảng C_V C_C có thể sẽ dịch ảnh.

\(M\xrightarrow[{{d_1};{d_1}'}]{{{L_1}}}{M_1}\xrightarrow[{{d_2};{d_2}'}]{{{L_2}}}M' \equiv {C_V}\)  

\(\begin{gathered}
{d_2}' = - O{C_V} \to \infty \hfill \\
{d_2} = {f_2} = 4cm \hfill \\
{d_1}' = l - {d_2} = 20 - 4 = 16cm \hfill \\
{d_1} = \dfrac{{16.1}}{{15}} \approx 10,67mm \hfill \\ 
\end{gathered} \)

\(N\xrightarrow[{{d_1};{d_1}'}]{{{L_1}}}{N_1}\xrightarrow[{{d_2};{d_2}'}]{{{L_2}}}N' \equiv {C_C}\)

\(\begin{gathered}
{d_2}' = - {O_2}{C_C} = - 20cm \hfill \\
{d_2} = \dfrac{{20.4}}{{24}} = \dfrac{{10}}{3}cm \hfill \\
{d_1}' = l - {d_2} = 20 - \dfrac{{10}}{3} = \dfrac{{50}}{3}cm \hfill \\
{d_1} = \dfrac{{100}}{{94}} \approx 10,64mm \hfill \\ 
\end{gathered} \)      

 Vậy Δd = 0,03mm ≈ 30µm.

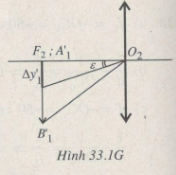
b) Khi ngắm chừng ở vô cực, ảnh A₁’B₁’ của vật tạo bởi vật kính ở tại tiêu diện vật của thị kính (Hình 33.1G).

Khoảng ngắn nhất trên A₁’B₁’ mà mắt phân biệt được:

Δy₁’ = f₂tanε = f₂ε

Suy ra khoảng ngắn nhất trên vật:

\(\Delta y =\dfrac{\Delta y_1'}{|k_1|}=\dfrac{f_2.\epsilon}{|k_1|}=0,8 .10^{-6} m\)

soanvan.me