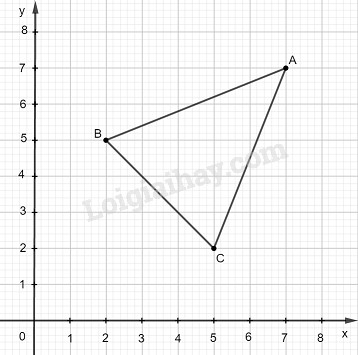
Trên mặt phẳng tọa độ \(Oxy\) cho ba điểm A, B, C có tọa độ như sau: A (7; 7), B(2, 5), C (5; 2).
LG a
Hãy viết phương trình các đường thẳng AB, BC, CA.
Phương pháp giải:
Để viết phương trình đường thẳng đi qua hai điểm cho trước ta thực hiện các bước sau:
Bước 1: Gọi phương trình đường thẳng là \(y = ax + b\).
Bước 2: Thay tọa độ các điểm thuộc đường thẳng, ta có các phương trình hai ẩn của \(a\) và \(b\).
Bước 3: Từ các phương trình tìm \(a\) và \(b\)
Bước 4: Kết luận phương trình đường thẳng với \(a\) và \(b\) đã tìm được.
Lời giải chi tiết:
+ Gọi phương trình đường thẳng AB là \(y = ax + b\).
Tọa độ của các điểm A, B thỏa mãn phương trình \(y = ax + b\) nên ta có:
\(\left\{ \begin{array}{l}
7 = a.7 + b\\
5 = a.2 + b
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
b=7-7a\\
b=5-2a
\end{array} \right.\)
Suy ra: \(7-7a=5-2a\)\(\Leftrightarrow 5a=2\Leftrightarrow a = \dfrac{2}{5}\)
\(\Rightarrow b =5-2a=5-2. \dfrac{2}{5}= \dfrac{{21}}{5}\)
Vậy phương trình đường thẳng AB là \(y = \dfrac{2}{5}x + \dfrac{{21}}{5}\)
+ Gọi phương trình đường thẳng BC là \(y = a'x + b'\).
Tọa độ của các điểm B, C thỏa mãn phương trình \(y = a'x + b'\) nên ta có:
\(\left\{ \begin{array}{l}
5 = a'.2 + b'\\
2 = a'.5 + b'
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
b' = 5-2a'\\
b' = 2-5a'
\end{array} \right.\)
Suy ra: \(5-2a'=2-5a'\)\(\Leftrightarrow 3a'=-3\Leftrightarrow a' = -1\)
\(\Rightarrow b =5-2a'=5-2. (-1)= 7\)
Vậy phương trình đường thẳng BC là \(y = -x + 7\).
+ Gọi phương trình đường thẳng AC là \(y = a''x + b''\).
Tọa độ của các điểm A, C thỏa mãn phương trình \(y = a''x + b''\) nên ta có:
\(\left\{ \begin{array}{l}
7 = a''.7 + b''\\
2 = a''.5 + b''
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
b'' = 7-7a''\\
b'' = 2- 5a''
\end{array} \right.\)
Suy ra: \(7-7a''=2-5a''\)\(\Leftrightarrow 2a''=5\Leftrightarrow a'' = \dfrac{5}{2}\)
\(\Rightarrow b'' =2-5a''=2-5. \dfrac{5}{2}= -\dfrac{{21}}{2}\)
Vậy phương trình đường thẳng AC là \(y = \dfrac{5}{2}x - \dfrac{{21}}{2}\)
LG b
Coi độ dài mỗi đơn vị trên các trục \(Ox\), \(Oy\) là \(1cm\), hãy tính chu vi, diện tích của tam giác ABC (lấy chính xác đến hai chữ số thập phân).
Phương pháp giải:
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có hệ thức:
\(A{B^2} + A{C^2} = B{C^2}\).
Chu vi tam giác bằng tổng ba cạnh.
Diện tích tam giác ABC được tính bằng hiệu diện tích hình vuông cạnh \(5cm\) trừ đi ba diện tích của các tam giác xung quanh.
Lời giải chi tiết:
Áp dụng định lí Pytago vào các tam giác vuông lần lượt có các cạnh huyền AB, AC, BC ta tính được độ dài các cạnh như sau:
\(AB =\sqrt{5^2+2^2}=\sqrt{29}\approx 5,39cm\)
\(AC =\sqrt{5^2+2^2}=\sqrt{29}\approx 5,39cm\)
\(BC =\sqrt{3^2+3^2}=\sqrt{18}\approx 4,24cm\)
Do đó chu vi của tam giác ABC là \( AB+AC+BC \approx 5,39+5,39+4,24\)\(=15,02cm\).
Diện tích tam giác ABC được tính bằng hiệu diện tích hình vuông cạnh \(5cm\) trừ đi ba diện tích của các tam giác xung quanh.
\({S_{ABC}} =5^2-\dfrac{1}2.5.2-\dfrac{1}2.5.2-\dfrac{1}2.3.3\)\(= 10,5(c{m^2})\)
soanvan.me
