Đề bài
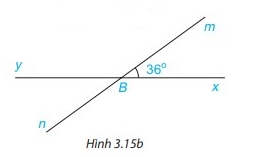
Cho Hình 3.15b, biết \(\widehat {xBm} = 36^\circ \). Tính số đo các góc còn lại trong hình vừa vẽ.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất:
+ Tổng của 2 góc kề bù là 180 độ.
+ 2 góc đối đỉnh thì bằng nhau.
Lời giải chi tiết
Vì \(\widehat{xBm}\) và \(\widehat{yBn}\) là hai góc đối đỉnh nên \(\widehat {xBm} = \widehat {yBn}\)
Mà \(\widehat {xBm} = 36^\circ \) nên \(\widehat {yBn} = 36^\circ \)
Vì \(\widehat{xBm}\) và \(\widehat{mBy}\) là hai góc kề bù nên
\(\begin{array}{l}\widehat {xBm} + \widehat {mBy} = 180^\circ \\ \Rightarrow 36^\circ + \widehat {mBy} = 180^\circ \\ \Rightarrow \widehat {mBy} = 180^\circ - 36^\circ = 144^\circ \end{array}\)
Vì \(\widehat{mBy}\) và \(\widehat{nBx}\) là hai góc đối đỉnh nên \(\widehat {mBy} = \widehat {nBx}\)
Mà \(\widehat {mBy} = 144^\circ \) nên \(\widehat {nBx} = 144^\circ \)
