Đề bài
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, ∠BAD = \(60^0\), SA = SB = SD = a.
a) Chứng minh (SAC) vuông góc với (ABCD).
b) Chứng minh tam giác SAC vuông.
c) Tính khoảng cách từ S đến (ABCD).
Lời giải chi tiết
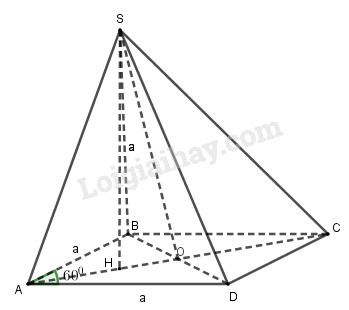
a) Nhận xét: Tam giác ABD là tam giác đều.
Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:
SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ H là trọng tâm tam giác ABD
⇒ H ∈ AC.
\( \Rightarrow SH \subset \left( {SAC} \right)\)
Mà \(SH \bot \left( {ABCD} \right)\) \( \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\)
b) AO là đường cao trong tam giác đều ABD cạnh a nên \(AO = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow AH = \dfrac{2}{3}AO\) \( = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3}\)
Ta có: \(HC = AC - AH = 2AO - AH\) \( = 2.\dfrac{{a\sqrt 3 }}{2} - \dfrac{{a\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}\)
\( \Rightarrow SC = \sqrt {S{H^2} + H{C^2}} \) \( = \sqrt {\dfrac{{6{a^2}}}{9} + \dfrac{{12{a^2}}}{9}} = a\sqrt 2 \)
Tam giác SAC có:
\(S{A^2} + S{C^2} = {a^2} + 2{a^2} = 3{a^2}\) và \(A{C^2} = {\left( {2AO} \right)^2} = {\left( {2.\dfrac{{a\sqrt 3 }}{2}} \right)^2} = 3{a^2}\)
Do đó \(S{A^2} + S{C^2} = A{C^2}\) hay tam giác vuông tại S.
c) Ta có: \(SH \bot \left( {ABCD} \right)\) \( \Rightarrow d\left( {S,\left( {ABCD} \right)} \right) = SH = \dfrac{{a\sqrt 6 }}{3}\)
soanvan.me
