Bài 4 trang 148 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Cho tam giác ABC có ba góc nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt AB tại E và cắt AC tại F. Gọi H là giao điểm của BF và CE.

a) Chứng minh rằng bốn điểm A, E, H, F cùng thuộc một đường tròn.

b) Gọi I là trung điểm của AH. Chứng minh rằng \(OI \bot EF\).

c) Gọi D là giao điểm của AH với BC. Chứng minh rằng : HA.HD = HB.HF = HC.HE

d) Chứng minh rằng IF là tiếp tuyến của đường tròn (O).

e) Chứng minh rằng H là tâm đường tròn nội tiếp tam giác DEF.

Lời giải chi tiết

 

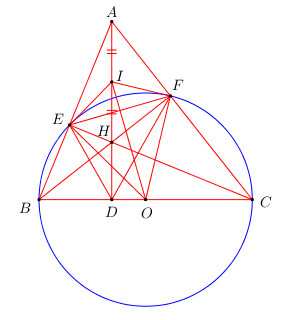
a) Vì \(\angle AEH = \angle AFH = {90^0} \Rightarrow E,\,\,F\) cùng thuộc đường tròn đường kính AH.

Vậy bốn điểm \(A,\,\,E,\,\,H,\,\,F\) cùng thuộc đường tròn đường kính \(AH\).

b) I là trung điểm của \(AH \Rightarrow I\) là tâm đường tròn đường kính \(AH\).

Mà \(E,\,\,F\) cùng thuộc đường tròn đường kính AH (cmt) \( \Rightarrow IE = IF \Rightarrow I\) thuộc đường trung trực của \(EF\).

Ta có \(OE = OF \Rightarrow O\) thuộc trung trực của \(EF\).

Do đó \(OI\) là trung trực của \(EF \Rightarrow OI \bot EF\).

c) Xét \(\Delta HBE\) và \(\Delta HCF\) ta có:

\(\angle HBE = \angle HCF\)(cùng phụ với \(\angle BAC\))

\(\angle BHE = \angle CHF\) (đối đỉnh)

\( \Rightarrow \Delta HBE \sim \Delta HCF\,\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{HB}}{{HC}} = \dfrac{{HE}}{{HF}} \)

\(\Rightarrow HB.HF = HC.HE\,\,\left( 1 \right)\).

Xét \(\Delta HAF\) và \(\Delta HBD\) có :

\(\angle AHF = \angle BHD\) (đối đỉnh) ;

\(\angle AFH = \angle BDH = {90^0}\) ;

\( \Rightarrow \Delta HAF \sim \Delta HBD\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{HA}}{{HB}} = \dfrac{{HF}}{{HD}}\)

\(\Rightarrow HA.HD = HB.HF\,\,\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow HA.HD = HB.HF = HC.HE\).

d) Xét \(\Delta OBF\) có \(OB = OF \Rightarrow \Delta OBF\) cân tại \(O \Rightarrow \angle OFB = \angle OBF\).

Mà \(\angle OBF = \angle CAD\) (cùng phụ với \(\angle ACB\))

\( \Rightarrow \angle OFB = \angle CAD\).

Xét tam giác vuông \(AFH\) có trung tuyến \(IF\) ứng với cạnh huyền \(AH \Rightarrow IF = IH = IA\)

\(\Rightarrow \Delta IFH\) cân tại \(I \Rightarrow \angle IFH = \angle IHF\).

\( \Rightarrow \angle IFH + \angle OFH = \angle IHF + \angle CAD \)

\(\Rightarrow \angle OFI = {90^0}\) \(\Rightarrow IF \bot OF\) tại \(F\).

Mà \(OF\) là bán kính của \(\left( O \right)\) nên \(IF\) là tiếp tuyến tại \(F\) của đường tròn \(\left( O \right)\).

e) Ta có : \(HB.HF = HC.HE\,\,\left( {cmt} \right)\)

\(\Rightarrow \dfrac{{HB}}{{HC}} = \dfrac{{HE}}{{HF}}\).

Xét \(\Delta HBC\) và \(\Delta HEF\) có :

\(\angle BHC = \angle EHF\) (đối đỉnh) ;

\(\dfrac{{HB}}{{HC}} = \dfrac{{HE}}{{HF}}\,\,\left( {cmt} \right)\) ;

\( \Rightarrow \Delta HBC \sim HEF\,\,\left( {c.g.c} \right) \)

\(\Rightarrow \angle HEF = \angle HBC;\,\,\angle HFE = \angle HCB\).

Hoàn toàn tương tự ta chứng minh được

\(\Delta HED \sim \Delta HAC\,\,\left( {c.g.c} \right) \)

\(\Rightarrow \angle HED = \angle HAC\).

\(\Delta HFD \sim \Delta HAB\,\,\left( {c.g.c} \right)\)

\(\Rightarrow \angle HFD = \angle HAB\).

Lại có \(\angle HBC = \angle HAC\) (cùng phụ với \(\angle ACB\))

\(\angle HCB = \angle HAB\) (cùng phụ với \(\angle ABC\))

\( \Rightarrow \angle HEF = \angle HED \Rightarrow HE\) là phân giác của \(\angle DEF\) (3).

\(\angle HFE = \angle HFD \Rightarrow HF\) là phân giác của \(\angle EFD\) (4).

Từ (3) và (4) \( \Rightarrow H\) là giao điểm 2 đường phân giác của \(\Delta DEF \Rightarrow H\) là tâm đường tròn nội tiếp \(\Delta DEF\).

 soanvan.me