Đề bài
Chứng minh rằng \(sin2(x + kπ) = sin 2x\) với mọi số nguyên \(k\). Từ đó vẽ đồ thị hàm số \(y = sin2x\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính tuần hoàn và chu kì của hàm số \(y = \sin x\): Hàm \(y = \sin x\) là hàm tuần hoàn với chu kì \(2\pi\).
Lời giải chi tiết
Hàm \(y = \sin x\) là hàm tuần hoàn với chu kì \(2\pi\) nên ta có:
\(\sin 2\left( {x + k\pi } \right) = \sin \left( {2x + k2\pi } \right) \)\(= \sin 2x\,\,\forall k \in Z\)
Ta có:
\(\begin{array}{l}f\left( x \right) = \sin 2x\\\Rightarrow f\left( {x + \pi } \right) = \sin 2\left( {x + \pi } \right) \\ = \sin \left( {2x + k2\pi } \right) = \sin 2x = f\left( x \right)\end{array}\)
\( \Rightarrow \) Hàm số \(y=sin2x\) tuần là hàm tuần hoàn với chu kì \(\pi\).
Xét hàm số \(y = \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\).
Ta lấy các điểm đặc biệt như sau:
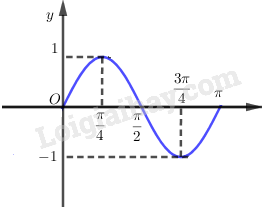
Từ đó ta có đồ thị hàm số \(y = \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\) là:
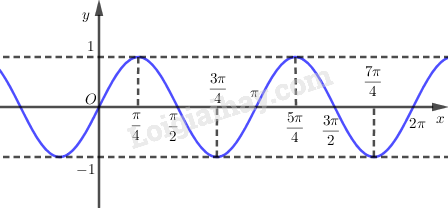
Do hàm số \(y = \sin 2x\) tuần hoàn với chu kì \(\pi \) nên ta có đồ thị là:
soanvan.me